Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 8 – vyšlo 18. února, ročník 20 (2022) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

8/2022

Kvantování prostoročasu – strašidelné působení na dálku

David Zoul

Šokující předpovědi kvantové mechaniky vedly řadu fyziků k přesvědčení, že kvantová teorie není úplnou teorií a že její pravděpodobnostní charakter je důsledkem existence skrytých proměnných, které pouze nejsme schopni identifikovat. Podle této myšlenky zdánlivě oddělené objekty ve skutečnosti mohou reagovat na určitý skrytý proces probíhající v pozadí. Velmi zjednodušenou analogií je stín tanečnice vrhaný reflektory na dvě plátna na opačných stranách jeviště. Oba stíny se mění současně podle pohybů tanečnice po jevišti. Pokud bychom byli schopni pozorovat pouze ony stíny, zdálo by se, že spolu interagují jakýmsi mysteriózním způsobem. Ve skutečnosti však pouze reagují na základnější proces probíhající v pozadí.

Tanečnice a stíny

Spin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole. Provázaný stav – entanglement, kvantově korelovaný stav systému dvou a více částic, v němž nemá smysl mluvit o stavech jednotlivých složek. Například z provázaného stavu dvojice fotonů nelze vyjádřit stavy jednotlivých fotonů. Značíme |AB>+|XY>, což znamená, že najdeme-li první částici ve stavu A, je druhá ve stavu B. Je-li první ve stavu X, pak druhá je ve stavu Y. Měřením provedeným na jedné částici se dozvíme určitou informaci o částici druhé. Je to způsobeno tím, že mají společnou minulost. Někdy se také hovoří o propletených stavech. EPR paradox – paradox kodaňské interpretace kvantové teorie zveřejněný v roce 1935 Albertem Einsteinem, Borisem Podolskym a Nathanem Rosenem. Podle něho by pro částice se společným původem mohlo dojít k tomu, že měření na jedné částici okamžitě ovlivní stav druhé částice. Einstein viděl řešení tohoto působení na dálku v neúplnosti kvantové teorie a předpokládal, že existují skryté parametry, které v experimentu nejsou uvažovány. V letech 1976 až 1983 byla existence lokálních skrytých parametrů experimentálně vyvrácena na základě Bellových nerovností. AB experiment – experiment, který navrhli v roce 1959 Yakir Aharonov a David Bohm. Experiment měl prokázat nesilové a nelokální působení magnetického pole soustředěného v ose solenoidu na chování elektronu vně solenoidu, kde je pole nulové. K interakci dochází ovlivněním fáze vlnové funkce elektronu v topologicky vícenásobně souvislé oblasti. Tento jev zřetelně ukazuje na kalibrační původ elektromagnetizmu. Experimentálně byl jev prokázán v roce 1986 Akira Tonomarou.

Problém nelokálnosti v kvantové teorii

K nejznámějším příznivcům teorie skrytých proměnných patřili například Albert Einstein, Luis de Broglie, Erwin Schrödinger, Erwin Madelung a David Bohm. V roce 1935 publikovala trojice autorů Albert Einstein, Boris Podolsky a Nathan Rosen myšlenkový experiment, který vešel ve známost podle iniciál příjmení autorů jako EPR paradoxEPR paradox – paradox kodaňské interpretace kvantové teorie zveřejněný v roce 1935 Albertem Einsteinem, Borisem Podolskym a Nathanem Rosenem. Podle něho by pro částice se společným původem mohlo dojít k tomu, že měření na jedné částici okamžitě ovlivní stav druhé částice. Einstein viděl řešení tohoto působení na dálku v neúplnosti kvantové teorie a předpokládal, že existují skryté parametry, které v experimentu nejsou uvažovány. V letech 1976 až 1983 byla existence lokálních skrytých parametrů experimentálně vyvrácena na základě Bellových nerovností.. Z této geniální myšlenkové konstrukce jednoznačně vyplynulo, že je-li kvantová mechanika úplnou teorií, potom musí být závislá na skutečnosti, kterou Einstein nazval strašidelným působení na dálku.

Louis Victor Pierre Raymond, vévoda de Broglie (1892–1987);
Erwin Rudolf Josef Alexander Schrödinger (1887–1961)

Erwin Madelung (1881–1972); Boris Podolsky (1896–1966)

Pokusím se nyní v krátkosti nastínit, o co v EPR konstrukci vlastně jde. Jak již víme, kvantová mechanika předpovídá, že žádná kvantová vlastnost neexistuje a priori, dokud ji měřícím zařízením nezaznamenáme. Vzpomeňme například Feynmanovo sčítání přes historieFeynmanův integrál – matematická metoda, při níž se nechá kvantový systém z výchozího klasického uspořádání propagovat po všech přípustných klasických trajektoriích. Každé takové klasické trajektorii přísluší komplexní váha, která odpovídá amplitudě pravděpodobnosti (A ~ exp[iS/ħ], kde S je akce dané trajektorie). Po čase t se spočtou celkové amplitudy možných klasických stavů od všech drah, které v těchto stavech končí. Jejich čtverce pak reprezentují pravděpodobnosti nalezení těchto stavů v okamžiku měření. Čtverec komplexní amplitudy tedy udává míru na prostoru všech možných klasických trajektorií., které přímo využívá skutečnosti, že před aktem měření se částice nalézá ve směsici (fyzikové říkají superpozici) všech možných stavů, z nichž kterýkoli by mohl být principiálně naměřen.

Nejinak je tomu i se spinemSpin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole., který můžeme u nabitých částic měřit tím, že je necháme projít nehomogenním magnetickým polem a poté dopadnout na fotografickou desku, jako to učinili roku 1921 Otto Stern a Walther Gerlach. Co si ale počít s měřením spinu u částic, které jsou bez náboje a přítomnost magnetického pole tudíž příliš necítí? Co když budeme chtít měřit spin třeba u fotonů? Možná vás překvapí, že je to dokonce ještě jednodušší a v dnešní době si takový experiment může téměř každý udělat v domácích podmínkách. Není k tomu vůbec zapotřebí specializovaná laboratoř plná drahého vybavení.

Otto Stern (1888–1969), Walther Gerlach (1889–1979)

Každý z vás byl již jistě někdy ve 3D kině, kde si za symbolický poplatek zakoupil 3D brýle. Pokud jste šli s partnerem/partnerkou, dostali jste tedy dvoje 3D brýle, což pro náš experiment postačí. 3D kino je založeno na promítání dvojice navzájem posunutých obrazů (sejmutých původně dvojicí kamer) na plátno, přičemž každý z obrazů nesou fotony s jinou projekcí svého spinu čili tzv. polarizací. Jestliže je např. levý z obrazů polarizován horizontálně, pravý bude polarizován vertikálně. V brýlích jsou vsazeny tzv. polarizační filtry, které mají schopnost propouštět vždy jen fotony s určitou polarizací (s určitou projekcí svého spinu). V každých brýlích je vždy před jedním okem polarizační filtr propouštějící fotony s horizontální polarizací a před druhým okem polarizační filtr pootočený o 90°, který tudíž propouští pouze fotony s vertikální polarizací. Právě použití polarizačních filtrů zajistí, že každé oko uvidí jen jeden z dvojice různě polarizovaných obrazů, které jsou promítány na plátno. Touto iluzí vzniká v mozku vjem stereoskopického (binokulárního) vidění neboli vnímání 3D obrazu. Na obdobných principech fungují také například 3D televizory.

Pokud vyndáte z brýlí obě polarizační fólie a dáte je za sebe, žádné fotony neprojdou skrz. První fólie totiž propustí pouze fotony s jednou polarizací, které však druhá fólie (propouštějící pouze fotony s kolmou polarizací) všechny pohltí. Jakmile jednu z fólií o malý úhel pootočíte, pravděpodobnost průchodu fotonu se stane nenulovou a vy opět skrz fólie trochu uvidíte. Pokud ji pootočíte o úhel 90°, bude intenzita procházejícího světla maximální.

Toto si lze zatím intuitivně celkem dobře představit. Modifikujme nyní ale náš experiment tím, že mezi dvě kolmo polarizující fólie (které tedy nepropustí dohromady žádné fotony) vložíme ještě jednu polarizační fólii (vyndanou z těch druhých brýlí), avšak pootočenou o 45°. Zdravý rozum velí, že pokud již tak neprůhledný materiál doplníme ještě dalším filtrem, světlo už nemá tuplem šanci projít skrz. Jenomže spoléhat se v moderní fyzice na zdravý rozum je věc ošemetná a ani tento případ nebude výjimkou. Vložení třetí fólie paradoxně způsobí, že fotony začnou systémem filtrů opět procházet.

Vysvětlení tohoto nanejvýš podivného výsledku opět přináší kvantová mechanika. Projekce spinu nemá nikdy úplně ostrou hodnotu – je superpozicí všech možných projekcí, které vystupují ve vlnové funkci fotonu s různými pravděpodobnostmi. Pokud dva polarizační filtry navzájem pootočíme o 45°, klesne pravděpodobnost průchodu fotonu na 50 % původní pravděpodobnosti, kdy dvojice filtrů propouštěla maximum fotonů. V tomto uspořádání tedy projde jen polovina fotonů – obraz ztmavne, ale stále bude viditelný. Při dalším pootočení o 45° by měla pravděpodobnost klesnout o zbylých 50 %, takže by měl obraz úplně zmizet. Tak tomu skutečně je, pokud použijeme jen dvě fólie.

Přidání třetí fólie, však celou situaci mění – průchod fotonů skrz každou z fólií lze totiž považovat za akt měření, který vymaže informaci o předešlé historii každého z fotonů a vytváří nový výchozí stav. Jestliže tedy máme tři fólie navzájem vůči sobě pootočené o 45°, pak druhá fólie zredukuje počet fotonů na 50 % z počtu fotonů, které prošly první fólií, třetí fólie pak opět zredukuje počet fotonů na 50 % z počtu fotonů, které prošly druhou fólií. Celkově tedy naší trojicí filtrů projde 25 % z počtu fotonů, které propustil první filtr.

Pokud jste si experiment sami provedli, snad vás přesvědčil, že každá částice se až do aktu měření skutečně nalézá v superpozici různých projekcí svého spinu a teprve aktem měření náhodně rozhodneme, která orientace spinu se u té, které částice skutečně měřitelně projeví. Tak, jako jsme pootočením polarizačního filtru o 45° náhodně rozhodli, které fotony projdou a které filtr pohltí. Měřením spinu zároveň vytváříme novou superpozici, takže jakmile u téže částice budeme následně měřit spin v jiném směru (například pootočeném o dalších 45°), opět nevíme předem nic o tom, jakou projekci spinu naměříme tentokrát (které fotony projdou a které budou pohlceny ve třetím polarizátoru).

Představme si nyní, že máme dva elektrony na stejné energetické hladině v nějakém atomu. Pauliho vylučovací principPauliho vylučovací princip – „Dva fermiony nemohou být nikdy ve stejném kvantovém stavu“. Právě proto různé elektrony v atomárním obalu zaujímají různé kvantové stavy a tím vytvářejí různorodé chování chemických prvků. striktně nařizuje, že aby vedle sebe mohly existovat dva fermionyFermiony – částice, které mají poločíselný spin, vlnová funkce je antisymetrická, splňují Pauliho vylučovací princip a podléhají Fermiho–Diracovu statistickému rozdělení. Patří mezi ně všechny leptony, kvarky a baryony – například elektron, neutrino, proton a neutron. Při nízkých teplotách fermiony obsazují stavy postupně, až po tzv. Fermiho mez., nemohou mít všechna kvantová čísla stejná. Dva elektrony sedící na stejné hladině se tak vždy musí lišit alespoň projekcí svého spinu. O takovýchto dvou elektronech s navzájem korelovanými spiny říkáme, že jsou entanglované (propletenéProvázaný stav – entanglement, kvantově korelovaný stav systému dvou a více částic, v němž nemá smysl mluvit o stavech jednotlivých složek. Například z provázaného stavu dvojice fotonů nelze vyjádřit stavy jednotlivých fotonů. Značíme |AB>+|XY>, což znamená, že najdeme-li první částici ve stavu A, je druhá ve stavu B. Je-li první ve stavu X, pak druhá je ve stavu Y. Měřením provedeným na jedné částici se dozvíme určitou informaci o částici druhé. Je to způsobeno tím, že mají společnou minulost. Někdy se také hovoří o propletených stavech.).

Autoři EPREPR paradox – paradox kodaňské interpretace kvantové teorie zveřejněný v roce 1935 Albertem Einsteinem, Borisem Podolskym a Nathanem Rosenem. Podle něho by pro částice se společným původem mohlo dojít k tomu, že měření na jedné částici okamžitě ovlivní stav druhé částice. Einstein viděl řešení tohoto působení na dálku v neúplnosti kvantové teorie a předpokládal, že existují skryté parametry, které v experimentu nejsou uvažovány. V letech 1976 až 1983 byla existence lokálních skrytých parametrů experimentálně vyvrácena na základě Bellových nerovností. uvažovali následovně: Rozdělme tyto elektrony a předejme jeden z nich Alici a druhý Bobovi, kteří s nimi poté odletí kosmickým korábem na opačné konce Sluneční soustavy. Pokud si Alice s Bobem před svým startem seřídili hodinky, startovali ve stejný okamžik a po celou dobu letu se pohybovali stejnými rychlostmi, mají jistotu, že i na opačných stranách Sluneční soustavy jsou jejich hodinky stále synchronizované.

Předpokládejme ještě, že se před odletem dohodli na hodině, minutě a sekundě, kdy provedou oba naráz měření, každý na svém elektronu. Alice ani Bob předem neví, jakou projekci spinu naměří. Na tom by nebylo nic až tak divného – kdyby například vezli namísto elektronů zapečetěné obálky s binárními číslicemi 0 a 1 uvnitř, také by až do rozlepení obálek nevěděli, kterou číslici má každý z nich v obálce. Na rozdíl od zapečetěných obálek však elektrony až do aktu měření skutečně nemají jasně určenou projekci svého spinu. Vzpomeneme-li si na náš experiment s polarizačními filtry, o tom, která projekce spinu bude skutečně pozorována, rozhoduje náhoda v okamžiku měření. Až do tohoto okamžiku se dle kvantové mechaniky elektron nalézá v superpozici obou možných projekcí svého spinu. Přesto nám zákony kvantové mechaniky zaručují, že pokud byly projekce spinů elektronů jednou spárované (vzájemně opačné), zůstanou tak i poté, co byly elektrony přeneseny na opačné strany Sluneční soustavy.

Ve chvíli, kdy Alice provede měření na svém elektronu, dozví se okamžitě, jakou projekci spinu v tu samou chvíli naměřil Bob na opačné straně Sluneční soustavy, a naopak. Přesto, že světelný signál by napříč Sluneční soustavou cestoval až několik let (Oortův oblak, tvořící hranici Slunečního systému, má poloměr až 2 světelné roky). Elektrony přitom do poslední chvíle „nevěděly“ jakou projekci spinu každému z nich přírodní ruleta přidělí. Informace o konečné volbě projekce spinu se tak mezi oběma elektrony předala nadsvětelnou rychlostí. Ba co víc, přenesla se okamžitě.

Je to ale skutečně tak, nebo zde přeci jen může vstupovat do hry skrytá proměnná, vzájemně korelující stav obou entanglovaných elektronů a předem tajně rozhodující o tom, co Alice i Bob ve skutečnosti naměří? V roce 1964 odvodil irský fyzik John Bell sérii matematických nerovností, založených na obdobných tricích s pootáčením polarizačních filtrů, jaké jsme si předvedli výše. Přesné splnění těchto nerovností by znamenalo, že za zdánlivě náhodným chováním kvantového světa (jakým je například náhodná volba projekce spinu konkrétního elektronu v okamžiku jeho měření) ve skutečnosti stojí hlubší lokální deterministický proces probíhající skrytě kdesi v pozadí a že tedy kvantová mechanika je neúplnou teorií.

Popišme si stručně, jak Bellův nápad v základním principu funguje. Předpokládejme, že jsou oba entanglované elektrony předem naprogramovány tak, aby při měření spinu podél některé z os navzájem skloněných řekněme pod úhly 45°, každý z nich vykázal spin dle skrytého algoritmu. Tentýž program bude diktovat druhému z elektronů, aby při měření podél téže osy vykázal spin přesně opačný. Očíslujeme-li jednotlivé osy po řadě 1, 2, 3, může program přiřazovat jednotlivým osám prvního elektronu spiny například ↑, ↑, ↓, a stejným osám druhého elektronu spiny přesně opačné, tzn. ↓, ↓, ↑. Ve skutečnosti si lze představit i jiné algoritmy navzájem korelující spiny, vždy ale bude platit, že nejméně dva ze spinů každého elektronu budou orientovány stejným směrem.

Předpokládejme dále, že si Alice a Bob vybírají zcela náhodně, podél které osy bude jeden každý z nich provádět svá měření. Existuje tak celkem 9 možností, jak mohou svá měření uskutečnit. Přidržíme-li se výše zavedeného číslování os, potom těchto 9 možností je (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3). Z těchto devíti možností si povšimněme pěti – (1,1), (2,2), (3,3), (1,2), (2,1) – které způsobí, že Alice i Bob spatří vzájemně opačný spin. V prvních třech případech se oba náhodně rozhodli měřit podél téže osy, zbylé dvě kombinace mají za následek rovněž vzájemně opačný spin, a to z jednoduchého důvodu: měření probíhá podél tří os, zatímco spin může nabývat pouze dvou hodnot. Podél některých dvou ze tří měřených os tak bude naměřen tentýž spin – viz předchozí odstavec.

Jelikož pět je více než polovina z devíti, znamená to, že pro víc než 50 % případů naměří Alice a Bob navzájem opačné spiny entanglovaných elektronů. Pokud by naopak měla pravdu kvantová mechanika a spin elektronu podél každé z os nebyl předem dán – vzniká zcela náhodně až v okamžiku měření – nemůže již z principu existovat žádný lokální (omezený na každý jeden elektron) skrytý program (skrytá proměnná), jež by spiny dvou entanglovaných elektronů vzájemně koreloval. V takovém případě naměří Alice a Bob navzájem opačný spin v průměru u přesně 50 % případů a ve stejném počtu případů dojde naopak ke shodě v pozorované orientaci obou spinů.

Toto tzv. narušení Bellových nerovností by znamenalo, že žádná lokální skrytá proměnná (metaforicky řečeno „zapečetěná obálka s předem daným výsledkem uvnitř“) neexistuje a kvantová mechanika je vnitřně konzistentní teorií.

John Stewart Bell (1928–1990), Alain Aspect (*1947)

Na počátku 80. let minulého století provedl tým francouzských fyziků pod vedením Alaina Aspecta sérii přesných měření polarizačních stavů fotonů, ve kterých se statisticky významnou pravděpodobností skutečně potvrdili narušení Bellových nerovností, a tedy nelokální charakter kvantové mechaniky (Einsteinovo strašidelné působení na dálku).

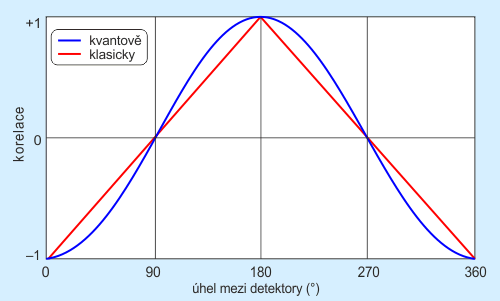
Obr. 1: Bellova klasická předpověď (červená křivka) versus změřený výsledek (modrá křivka) potvrzující narušení Bellových nerovností předpovídané kvantovou mechanikou

Pozornému čtenáři jistě neuniklo, že narušení Bellových nerovností ve skutečnosti nijak nevyvrací působení nelokálního skrytého procesu, který koreluje stavy entanglovaných elektronů na dálku, po vzoru naší tanečnice vrhající stín na dvě různá plátna. Zdá se, že minimálně ty objekty ve vesmíru, které spolu jedenkrát vešly v interakci (je jedno, zda si synchronizovaly své hodiny, nebo třeba spiny), zůstávají již nadále propojeny díky holografickémuHolografický princip – představa, že informace o N-dimenzionální entitě je zapsatelná v N−k dimenzích. Název pochází z holografie, v níž se informace o třírozměrném objektu zapisují na dvojrozměrném hologramu, z něhož je možné původní objekt rekonstruovat. V matematice jsou ze znalosti hodnot komplexní funkce mající derivaci (tzv. holomorfní funkce) na hranici množiny určitelné její hodnoty v celé množině. Ve fyzice jsou vlastnosti černé díry určeny pouze jejím povrchem. Holografický princip je velmi atraktivní ve fyzice elementárních částic a v některých teoriích gravitace. charakteru prostoru a neustále spolu zvláštním okamžitým způsobem komunikují. Je třeba hned zkraje upozornit, že tímto způsobem komunikace nelze přenášet žádné využitelné bity informací. Alice a Bob si nemohou nadsvětelnou rychlostí poslat žádnou zprávu například ve smyslu nějakého sdělení, které měli předem napsané na papírku. Mohou pouze současně získat informaci o tom, jaký spin elektronu právě naměřili.

Z Aspectova experimentu vyplývá, že se musíme zřeknout lokální skutečnosti a že buď svět „tam venku“ není skutečný, nebo že dochází k nějaké formě komunikace mnohem rychlejší než světlo (k Einsteinovu „strašidelnému působení na dálku“). Entanglovaný pár je tvořen jedinou vlnovou funkcí, která principiálně může být natažena přes celý vesmír. V okamžiku měření na jednom konci kolabuje tato vlnová funkce jako celek a pozorovatel na druhém konci se ihned dozvídá výsledek měření. Nejedná se o informaci v pravém slova smyslu, neboť výsledky měření nelze předem nijak ovlivnit, a tudíž touto cestou nelze přenášet zprávy a lorentzovská invariance není narušena. Jde o něco mnohem subtilnějšího, než je informace, ale přesto zřejmě zcela zásadního. V Lorentzových transformacích totiž vystupuje i časová složka, a právě čas se chová velmi podobně, jako onen entanglovaný pár v kvantové mechanice. Způsob, kterak se linie současnosti mezi vzdálenými objekty ve vesmíru neustále, a hlavně okamžitě přizpůsobují změnám jejich vzájemného potenciálu (funkce vzdálenosti a zrychlení) je doslova fascinující a velmi to opět připomíná strašidelné působení na dálku. Pokud vesmír nějak dokáže neustále, v každém okamžiku, „měřit“ polohu a změnu hybnosti každého objektu, na základě těchto hodnot stanovovat vzájemné potenciály jednotlivých objektů a jim přiřazovat odpovídající linie současnosti, lorentzovská invariance je tím automaticky zachována, nezávisle na existenci či neexistenci podkladové plochy. Pokud by však ona podkladová plocha byla schopna přenášet signály vysoce nadsvětelnou rychlostí, může být dokonce nutná k tomu, aby právě toto vesmír dokázal. Více se této otázce budeme věnovat v příštím, závěrečném dílu.

Pokud jednu částici páru nalezneme náhodně ve stavu A, zaujme v tom samém okamžiku druhá částice stav B, bez ohledu na jejich vzájemnou vzdálenost. Jakým kanálem se spolu dorozumívají? Kvantová mechanika nám tu ve skutečnosti poodhaluje jedno z největších tajemství vesmíru. Tímto problémem se zabývali po značnou část života například David Bohm, Richard Feynman, John Wheeler, John Crammer a řada dalších. Principielní problém přitom nepředstavuje princip neurčitosti, který je jen pouhým důsledkem hlubších zákonitostí, jimiž se řídí příroda. Zásadní otázkou spíše je, proč mají částice vlnovou, či vlny částicovou povahu, jaká je skutečná fyzikální podstata děje zvaného kolaps vlnové funkce a jak je možné, že probíhá v celém prostoru naráz. Je primární entitou korpuskule a vlnová funkce teprve čímsi, co okolo sebe korpuskule vytvářejí, či je primární entitou vlna a kvanta jsou pouhou iluzorní záležitostí vznikající v důsledku neschopnosti atomární látky (tvořené, hodně zjednodušeně řečeno, celočíselným násobkem půlvln) vysílat a přijímat energii jinak než po kvantech? Kvantová teorie na tyto otázky odpověď nezná, pouze nalezla vhodný matematický aparát simulující pozorované chování kvantových entit a schopný dávat poměrně rozsáhlé předpovědi, které jsou v souladu s pozorováním.

Výše jmenovaní autoři se však snažili nalézt fundamentálnější odpovědi, než je jen pouhá matematická simulace. David Bohm položil základy teorie pilotní vlny, která dává adekvátní kvantově mechanické předpovědi. V tomto modelu světa je primární entitou částice, která kolem sebe šíří vlnění podobně jako loďka na vodní hladině. Interakcí mnoha částic (například testovací částice + všechny částice tvořící experimentální aparaturu) dochází k interferenci vlnových příspěvků od každé ze zúčastněných částic (teoreticky od každé částice ve Vesmíru). Interferencí těchto vln vzniká v prostoru velmi složitý kvantový potenciál, který je obecně dosti obtížné spočítat a který nutí volnou testovací částici putovat mnohem pravděpodobněji v blízkosti minim tohoto potenciálu, nežli jeho maxim. Pro jednoduchá uspořádání, pro něž se podařilo kvantový potenciál nalézt, se výsledky nikterak nelišily od předpovědí klasické kvantové teorie. V této souvislosti se někdy hovoří o Vesmíru jako o gigantickém hologramu, v němž každá část je latentním obrazem celku.

Vlnovou funkci částice můžeme obecně napsat jako

\(\psi \left( {{\bf{r}},t} \right) = \sqrt {\rho \left( {{\bf{r}},t} \right)} \;\exp \left[ {{\rm{i}}\,\varphi \left( {{\bf{r}},t} \right)} \right]\,,\)

(1)

kde

\(\rho \left( {{\bf{r}},t} \right) = {\left| {\psi \left( {{\bf{r}},t} \right)} \right|^2}\)

(2)

je úměrná hustotě pravděpodobnosti a

\(\varphi \left( {{\bf{r}},t} \right) = \arg \left[ {\psi \left( {{\bf{r}},t} \right)} \right]\)

(3)

reprezentuje fázi vlnové funkce. Protože v řadě experimentů se zajímáme o \({\left| \psi \right|^2}\), zdálo by se, že fáze nehraje v kvantových procesech žádnou roli. Ve speciálně postavených interferenčních experimentech ji však přesto musíme brát v úvahu, jak se lze přesvědčit na příkladu Aharonova – Bohmova jevuAB experiment – experiment, který navrhli v roce 1959 Yakir Aharonov a David Bohm. Experiment měl prokázat nesilové a nelokální působení magnetického pole soustředěného v ose solenoidu na chování elektronu vně solenoidu, kde je pole nulové. K interakci dochází ovlivněním fáze vlnové funkce elektronu v topologicky vícenásobně souvislé oblasti. Tento jev zřetelně ukazuje na kalibrační původ elektromagnetizmu. Experimentálně byl jev prokázán v roce 1986 Akira Tonomarou.. Podobně je tomu rovněž v případě nízkoteplotních experimentů se supravodivými či supra­teku­tými kvantovými systémy. V dynamice těchto kvantových kapalin a v jejich topologických vlastnostech hraje fáze dokonce rozhodující roli. Tyto soustavy jsou popsány tzv. makroskopickou vlnovou funkcí, která má tvar formálně shodný s (1), avšak ρ je zde úměrné nikoliv pravděpodobnosti nalezení částice, nýbrž přímo hustotě kondenzátu neboli makroskopickému počtu částic v základním kvantovém stavu. Fázový faktor φ je pak makroskopickou fází tohoto kondenzátu. Makroskopická vlnová funkce tvoří základ fenomenologického popisu všech kvantových kapalin. Pokud se u těchto kapalin nalézá obrovský počet částic v jediném kvantovém stavu, dostává vlnová funkce ψ(r, t) klasickou interpretaci. Kondenzát pak můžeme považovat za makroskopickou kvantovou částici.

Vlnovou funkci ψ(r, t) je rovněž možno formulovat pomocí klasické akce S a poté definovat dráhu částice pomocí Hamiltonova principu jako trajektorii, podél níž je akce S minimální. Vlnová funkce má v tomto formalismu tvar

\[\psi = \left| \psi \right|\exp \left( {\frac{{{\rm{i}}\,S}}{\hbar }} \right) = \left| \psi \right|\exp \left( {{\rm{i}}\,\varphi } \right) = \sqrt \rho \exp \left( {\frac{{{\rm{i}}\,S}}{\hbar }} \right),\]

(4)

s jehož pomocí lze formulovat tzv. hydrodynamickou formu Schrödingerovy rovnice, kterou poprvé publikoval již v roce 1926 Erwin Madelung. Dosadíme-li do klasické Schrödingerovy rovnice vlnovou funkci (4), dostaneme dvě nelineární rovnice:

\[\frac{{\partial \rho }}{{\partial t}} + {\mathop{\rm div}\nolimits} \left( {\frac{\rho }{m}\nabla S} \right) = 0{\kern 1pt} ,\] \[\frac{{\partial S}}{{\partial t}} + \frac{1}{{2m}}{\left( {\nabla S} \right)^2} + {V} + {Q_m} = 0{\kern 1pt} ,\]

(5)

kde V je potenciální energie a Q_m je kvantový potenciál daný vztahem

\[{Q_m} = \frac{{{\hbar ^2}}}{m}\left( {\frac{{{\nabla ^2}\rho }}{\rho } + \frac{{{{\left( {\nabla \rho } \right)}^2}}}{{{\rho ^2}}}} \right)\,.\]

(6)

Položíme-li

\[{\bf{J}} = \frac{\rho }{m}\nabla S\,,\]

(7)

kde J značí proudovou hustotu částic, pak z první rovnice (5) dostaneme

\[\frac{{\partial \rho }}{{\partial t}} + {\rm{div}}\;{\bf{J}} = 0\,,\]

(8)

což je rovnice kontinuity známá z klasické hydrodynamiky (odtud pojmenování hydrodynamická forma Schrödingerovy rovnice), popřípadě elektrodynamiky (jedná-li se o proud nabitých částic). Druhá rovnice (5) odpovídá klasické Jacobiho rovnici, v níž se ovšem vyskytuje nový člen Q_m, tj. kvantový potenciál. Pro Q_m = 0 dostáváme rovnice klasické mechaniky. Kvantovou mechaniku tak můžeme interpretovat jako klasickou mechaniku doplněnou o kvantový potenciál Q_m, který závisí na hustotě částic ρ a jejím gradientu. Vlnovou funkci ψ pak můžeme interpretovat jako kvantové pole doprovázející každou jednotlivou částici, dynamika částic je řízena gradientem fáze či akce a proudová hustota bude dána vztahem

\[{\bf{J}} = \frac{\rho }{m}\nabla S = \frac{\hbar }{m}\nabla \varphi\,. \]

(9)

Hydrodynamická formulace Schrödingerovy rovnice, známá také jako mechanika s kvantovým potenciálem, smazává historicky vyhloubenou propast oddělující od sebe klasickou a kvantovou fyziku, zdůrazňujíc jednotu našeho světa.

Na výše popsanou Madelungovu interpretaci s kvantovým potenciálem již o rok později navázal Louis de Broglie ve své teorii pilotní vlny. Stalo se tak na proslulé Páté Solvayově konferenci, která se konala roku 1927 krátce po konečné formulaci kvantové mechaniky, jež vešla ve známost jako kodaňská (podle působiště jejího hlavního protagonisty Nielse Bohra). Vévoda de Broglie zde poprvé představil alternativní formulaci kvantové mechaniky, která byla vůbec první rigorózně formulovanou teorií skrytých proměnných. De Broglieova teorie řešila záhadu částice a vlny tím nejprostším způsobem: de Broglie postuloval existenci skutečné vlny i skutečné částice. Teorie byla založena na představě, že ačkoli je například elektron v podstatě klasickou částicí, jeho chování určuje tzv. pilotní vlna, která se řídí pravidly kvantové pravděpodobnosti a na elektron silově působí. Kvantové vlny spolu vzájemně interferují, čímž vznikají střídající se vzory maxim a minim, které pak ovlivňují pozorovatelný pohyb a uspořádání částic v prostoru prostřednictvím kvantového potenciálu, který na částice působí silou. Skrytou proměnnou je v této teorii přesná poloha částice.

Pole pilotních vln velkého souboru částic vytváří komplikovaný dynamický kvantový potenciál v celém prostoru, na který jsou citlivá všechna kvanta. Kvantový potenciál v okolí stínítka (filtru) se dvěma štěrbinami se bude lišit od kvantového potenciálu v okolí stínítka s jedinou otevřenou štěrbinou. Kvantum, které do takovéhoto prostředí vstoupí, se octne v jakémsi „morfogenetickém“ poli, které okamžitě reaguje na aktuální stav filtru. Částice tak bude setřásána do minim kvantového potenciálu a ta se budou u různých filtrů (s různým počtem štěrbin) pochopitelně lišit. To je důvod, proč přítomnost druhé štěrbiny ovlivňuje stav částice, která se při tom rozhodla projít pouze tou první.

Tato myšlenka se zdánlivě ocitla v kritických potížích, když v roce 1932 John von Neumann uveřejnil svoji převratnou knihu o kvantové teorii, která obsahovala mimo jiné i údajný „důkaz“, že žádná teorie se skrytými proměnnými nemůže náležitě popsat chování objektů v kvantovém světě. Protože byl von Neumann jedním z nejšpičkovějších matematiků své doby, nikoho nenapadlo hlouběji zkoumat jeho myšlenkový postup a existujících problémů v jeho argumentaci si tak zpočátku nikdo nevšiml.

Na vcelku školáckou chybu ve von Newmannově důkazu upozornila jako první matematička Grete Hermannová v roce 1935, podrobnější matematický rozbor celého von Neumannova omylu pak zveřejnil John Bell dokonce až v roce 1966.

John von Neumann (1903–1957), Grete Hermann (1901–1984)

Začátkem 50. let minulého století se americký fyzik David Bohm spolu s dalšími badateli pustili do rozvoje takové interpretace kvantové mechaniky, která se nese v duchu teorií skrytých proměnných a funguje přitom v konfrontaci s experimentální realitou stejně dobře, jako klasická kodaňská interpretace. Nicméně pohled na kvantovou skutečnost, jejž skýtá, je zcela odlišný. Bohm tento svůj pohled na podstatu skutečnosti shrnul v knize The Ghost in the Atom.

Podle Bohmovy interpretace mají částice vždy ostrou hodnotu polohy i hybnosti, avšak jakýkoliv pokus o jejich změření rozmaže tyto informace změnou pilotní vlny související s částicemi. „Šťouchnutí“ do pilotní vlny na jednom místě (například změřením polohy elektronu) okamžitě změní tvar pilotní vlny všude jinde, což ovlivní všechny částice ve sféře jejího působení. Protože způsob, jakým pilotní vlna ovlivňuje částice, určuje zpětně její tvar, nezáleží na tom, jak silná vlna na tom či onom místě je. Dokud do příslušného místa vlna zasahuje, změna jejího tvaru ovlivňuje všechny tamní částice. Klíčové přitom je, že pilotní vlna na poruchu v jednom konkrétním místě reaguje okamžitě v celém svém objemu. Sama pilotní vlna má tedy nelokální charakter.
Bell v roce 1966 dokázal, že teorie skrytých proměnných mohou fungovat právě za předpokladu nelokálnosti. Zároveň ale ukázal, že nelokálnost musí zahrnovat dokonce každá myslitelná interpretace kvantové reality. Bell v tomto roce publikoval své slavné nerovnosti, jejichž narušení znamenalo, že je jednou pro vždy potřeba zavrhnout pojem lokální skutečnosti. Slovo „lokální“ v této souvislosti znamená, že neexistuje žádná komunikace rychlejší než světlo ve vakuu a slovem „skutečnost“ je míněna existence světa nezávisle na našich pozorováních. Jakmile bylo experimentálně potvrzeno, že příroda vskutku Bellovy nerovnosti porušuje, bylo ihned zřejmé, že se musíme minimálně jednoho z těchto dvou pojmů vzdát.

Máme-li být úplně přesní, pak Bellova nerovnost ve skutečnosti vlastně vůbec nezávisí na kvantové mechanice. Porušení Bellových nerovností vyžaduje zavržení lokální skutečnosti dokonce i v případě, že by se časem kvantová mechanika ukázala býti neúplnou teorií. Vlnová funkce, ačkoliv zřejmě stojí v samých základech fyzikální reality, se sama poněkud vymyká čemukoli, co jsme zvyklí nazývat fyzikálním systémem. Jednak není přímo pozorovatelná – lze ji detekovat pouze pomocí částic. Na tom by nebylo nic až tak zvláštního – například fyzikální pole lze detekovat rovněž jen s pomocí testovacích částic. Mnohem závažnější vlastností vlnové funkce je právě skutečnost, že se může měnit v celém prostoru naráz. Změny se v ní šíří takovou závratnou rychlostí, že v rámci přesnosti našeho měření času dané Planckovou škálou, nastávají v celém prostoru jakoby současně.

Bohm myšlenku, že vše je propojeno se vším, jakož i okamžitě ovlivňováno veškerými událostmi ve vesmíru prostřednictvím pilotní vlny, dále rozvinul. Vystoupil s názorem, že zdánlivě nezávislé objekty ve skutečnosti reagují na určitý proces, který probíhá v pozadí.

John Bell později navrhl, aby se de Broglieova teorie se všemi důsledky z ní plynoucími nazývala „theory of beable variables“ (veličin existujících nezávisle na pozorování), v protikladu k „theory of observable variables“ (veličin vznikajících až coby důsledek pozorování), jíž prosazoval Niels Bohr. Tzv. de Broglieova-Bohmova formulace kvantové mechaniky tvoří jeden z přístupů k základům kvantové mechaniky, který je dnes předmětem stoupajícího zájmu.

Niels Henrick David Bohr (1885–1962), David Joseph Bohm (1917–1992),
Yakir Aharonov (*1932)

Na rozdíl od „theory of observable variables“ činí tato teorie víc, než jen pouhé statistické předpovědi – dopodrobna totiž popisuje, co se děje v každém jednotlivém experimentu. Vlna při svém vývoji v čase ovlivňuje pohyb částice a při tom porušuje relativitu současnosti, neboť zákon, který určuje vliv vlny na částici, může platit pouze v jediném souřadnicovém systému. Má-li to celé dávat smysl, musí existovat preferovaná soustava, jejíž hodiny odměřují preferovaný čas.

Dokud kontrolujeme předpovědi kvantové mechaniky jen na statistické úrovni, nemusíme se ptát, jak byly tyto korelace ve skutečnosti ustanoveny. Jakmile se ale snažíme pokročit od statistické předpovědi k příčinám, tj. k teorii skrytých proměnných, dochází ke konfliktu s relativitou současnosti. Aby teorie skrytých proměnných fungovala, musí přijmout definici současnosti pouze jediného – preferovaného – pozorovatele (rozuměj preferované soustavy). To ale navrací zpět do hry koncept absolutního klidu a absolutního pohybu, který zde existoval před Einsteinem.

Co kdyby Einstein nikdy nežil?

První experimentální výsledky svědčící o tom, že náležité vysvětlení chování světla vyžaduje dramatickou změnu způsobu, jakým do té doby fyzikové na svět nahlíželi, se objevily již v roce 1887, kdy Michelson a Morley oznámili své definitivní experimentální výsledky. V těchto experimentech spolu interferovaly dva navzájem kolmé paprsky světla. Pokud by ve směru pohybu Země okolo Slunce byla jiná rychlost světla než kolmo na tento směr, výsledný interferenční obrazec by se měnil během pootáčení celé aparatury o různé úhly. Nic takového ale nenastalo.

Albert Abraham Michelson (1852–1931), Edward Williams Morley (1838–1923)

V roce 1889 nabídl irský fyzik George Fitzgerald vysvětlení výsledků Michelsonova-Morleyova experimentu. Okolnost, že se při tomto experimentu nepodařilo naměřit jakoukoli změnu rychlosti světla s ohledem na směr, kterým se světlo pohybovalo relativně k Zemi, mohla být podle něj důsledkem smršťování celé experimentální aparatury (i samotné Země) ve směru pohybu. Problém by to vyřešilo, neboť by tak rychlost světla relativně k Zemi sice závisela na pohybu Země „éterem“, ale měřící aparatura by se smršťovala přesně v potřebné míře, aby to vyvolalo iluzi, že rychlost světla je stále c.

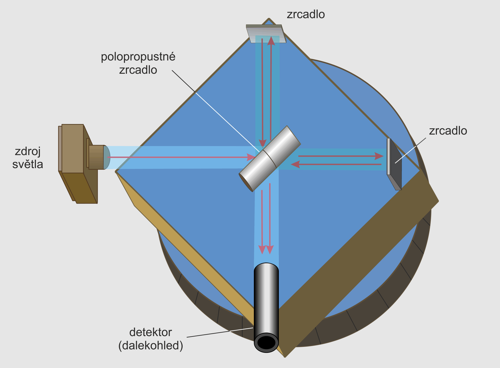
Obr. 2: Schéma Michelsonova-Morleyova experimentu

V 90. letech 19. století stejnou myšlenku nezávisle předložili i Hendrik Lorentz a Jules Henri Poincaré, dovedli ji však mnohem dále než Fitzgerald. V roce 1904 odvodil Lorentz soubor rovnic známý jako Lorentzovy transformace, jež popisují, jak se z pohledu pozorovatelů, kteří se pohybují odlišnými rychlostmi, transformují nejen délka pohybujícího se tělesa, nýbrž i čas a další veličiny. Své transformační rovnice Lorentz odvodil proto, aby matematicky popsal, jak by se elektromagnetická pole jevila různým pozorovatelům. Tyto transformace totiž do Maxwellových rovnic vkládají relativní rychlosti pozorovatelů.

O rok později Albert Einstein ukázal, že tytéž transformační rovnice se hodí i pro popis mechanických systémů a jejich transformací z pohledu pozorovatelů pohybujících se různými rychlostmi. Ukazují, jak se z pohledu různě rychlých pozorovatelů jeví odlišně nejen délka a čas, nýbrž také rychlost a dokonce i hmotnost, hybnost a energie pohybujících se těles. Lorentzovy výzkumy elektromagnetismu Einsteinovi posloužily coby odrazový můstek při odvozování speciální teorie relativity. Klíčovým pojmem speciální teorie relativity je předpoklad, že vesmír a fyzikální zákony by se měly jevit stejné všem pozorovatelům, nehledě na to, jak se pohybují. Tento předpoklad je znám jako Lorentzova invariance.

Bell poukázal na možnost, že „nejlacinějším řešením“ celé záhady kvantového světa je návrat k tomu druhu relativity, který existoval před Einsteinovou verzí, tedy k teorii, kterou vytvořili vizionáři jako Fitzgerald, Lorentz a Poincaré na základě předpokladu o reálné existenci „éteru“, to jest absolutního prostoru, na jehož pozadí probíhají veškeré fyzikální procesy.

George Francis FitzGerald (1851–1901), Jules Henri Poincaré (1854–1912),
Hendrik Antoon Lorentz (1853–1928)

Dle těchto úvah tzv. preferovaná souřadnicová soustava vskutku existuje, ale naše měřicí přístroje jsou pohybem zdeformovány právě tak, aby to zajistilo, že se nám nikdy nepodaří detekovat žádný pohyb „absolutním prostorem“ (nebo „relativně k němu“). Existence pre­fe­ro­vané soustavy souřadnic má velmi zajímavý důsledek: Přestože se věci v této soustavě mohou pohybovat rychleji než světlo, v os­tat­ních souřadnicových soustavách, ve kterých se vlivy šíří jak rychleji než světlo, tak zpátky v čase, je to jenom určitým druhem optické iluze. Pakliže existuje preferovaná soustava souřadnic, hodiny v této soustavě budou odtikávat preferovanou rychlostí času. Jedním rázem se tím obnovují jak Newtonův absolutní prostor, tak jeho absolutní čas. Pouze v Einsteinově verzi relativity, ve které jsou všech­ny souřadnicové soustavy vzájemně ekvivalentní, platí, že pohyb rychlejší než světlo znamená rovněž „skutečný“ pohyb zpátky v čase.

Bell tyto představy rozvinul v knize Speakable and Unspeakable in Quantum Mechanics. Ukázal, jak použití předeinsteinovské myšlenky preferované soustavy souřadnic, kombinované s experimentálním faktem, že pohyb relativně k této soustavě souřadnic nepozorujeme, vede k obvyklé formě Lorentzových transformačních rovnic, takže nelze experimentálně určit, která ze dvou rovnoměrně se pohybujících soustav je opravdu v klidu a která se pohybuje.

Poukáži v této souvislosti ještě na jednu záhadu, která znepokojuje vědce po řadu desetiletí – záhadu setrvačnosti. Má-li těleso změnit směr svého pohybu, nebo se začít pohybovat rychleji či pomaleji – na to vše je potřeba energie. Ale jak vlastně objekt „ví“, že se jeho pohyb mění (nebo nemění)? V takovém vesmíru, jaký známe, se chování těles podle všeho jeví jakoby svoji rychlost „měřila“ vzhledem k průměrné poloze (resp. k těžišti) veškeré hmoty ve vesmíru. Známo je to jako Machův princip. Einsteina tento princip při jeho formulaci obecné teorie relativity výrazně ovlivnil. Je ovšem poněkud ironií, že přes veškeré Einsteinovy snahy obecná teorie relativity ve skutečnosti Machův princip či původ setrvačnosti nevysvětluje. Má-li však Machův princip jakýkoli pravdivý základ, pak ve vesmíru existuje preferovaná souřadnicová soustava.

Ernst Mach (1838–1916) v různých obdobích. Napravo jeho známý autoprotrét.

Víme, že se vesmír rozpíná. Preferovanou souřadnicovou soustavou, specifikovanou průměrným rozložením veškeré hmoty ve vesmíru, je pak ta, ve které toto rozpínání probíhá dokonale rovnoměrně do všech směrů. Víme též, že v prvních okamžicích svého zrodu byl vesmír vyplněn superhorkou „polévkou“ elektromagnetického záření. Toto záření od té doby natolik ochladlo, že se přeměnilo ve slabý mikrovlnný rádiový šumReliktní záření – záření, které se od látky oddělilo přibližně 400 000 let po vzniku vesmíru, v době, kdy se vytvářely atomární obaly prvků a končilo plazmatické období vesmíru. Počáteční horkou (plazmatickou) fázi existence vesmíru nazýváme Velký třesk a reliktní záření tedy pochází z období konce Velkého třesku. Dnes má teplotu 2,73 K a vlnovou délku v milimetrové oblasti. Je jedním ze základních zdrojů informací pro naše poznání raného vesmíru. V anglické literatuře se označuje zkratkou CMB (Cosmic Microwave Background, mikrovlnné záření pozadí). o teplotě něco málo pod 3 K, dodnes takřka rovnoměrně vyplňující celý vesmír. Pozorovatel se tudíž nachází v klidu vůči preferované souřadnicové soustavě vesmíru i tehdy, když se nepohybuje relativně k reliktnímu záření kosmického pozadí. Preferovanou souřadnicovou soustavu nám tak nabízí dokonce samotné elektro­magne­tické pole. Například Sluneční soustava se v současnosti pohybuje vůči prostoru rychlostí 400 km/s ve směru souhvězdí Lva.

Tento pohyb vůči absolutnímu prostorovému pozadí je dobře viditelný na počítačově neupravených snímcích ze sond WMAPWMAP – Wilkinson Microwave Anisotropy Probe, sonda z roku 2001, která pořídila podrobnou mapu fluktuací reliktního záření s úhlovým rozlišením kolem 15′ a citlivostí 20 μK. Zrcadlo sondy mělo rozměry 1,4×1,6 m a teplota chlazené části byla nižší než 95 K. Data sondy jsou důležitým zdrojem informací o raných fázích vývoje vesmíru, většinou se kombinují s daty z pozemských zařízení jako je CBI a ACBAR a s daty z novější sondy Planck. Sonda byla umístěna v Lagrangeově bodě L2 soustavy Země-Slunce, kde pracovala do 28. října 2010. a PlanckPlanck – mikrovlnná observatoř evropské kosmické agentury ESA, která byla vynesena do vesmíru 14. května 2009. Byla určena k výzkumu fluktuací reliktního záření a monitorování vesmíru v mikrovlnné oblasti. Měla úhlovou rozlišovací schopnost 5′ a teplotní citlivost 2 μK. Oblohu snímkovala v devíti frekvenčních pásmech od 30 do 857 GHz (0,2 až 10 mm). Zrcadlo sondy mělo rozměry 1,9×1,5 m. Teplotu vysokofrekvenční části ohniska se podařilo po dobu dvou let udržet na extrémně nízké hodnotě 0,1 K. Činnost sondy byla ukončena v říjnu 2013., které přinesly dosud nejpřesnější snímky této kosmické radiace, jež je reliktem po horkém období vesmíru krátce po velkém třesku. Modrá oblast na obr. 3 je dopplerovský modrý posuv reliktního záření o 4 mK směrem k vyšším teplotám (kratším vlnovým délkám) oproti průměrné hodnotě, způsobený relativním pohybem (přibližováním se) Sluneční soustavy vzhledem k této oblasti ve Vesmíru. Obdobně červená oblast na opačné straně vesmíru je dopplerovský červený posuv reliktního záření o 4 mK směrem k nižším teplotám (větším vlnovým délkám), způsobený vzdalováním se Sluneční soustavy od tohoto místa na obloze.

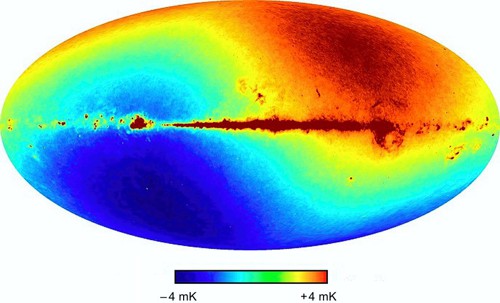
Obr. 3: Dopplerovský záznam pohybu Sluneční soustavy vzhledem
k reliktnímu pozadí vesmíru. Zdroj: WMAP.

Horká linie uprostřed snímku představuje další rušivý element způsobený zářením hvězd v rovině naší vlastní Galaxie, která tvoří tenký disk, skrz který hledíme do hlubokého vesmíru. Veškeré tyto efekty je potřeba nejprve odečíst, abychom nakonec získali čistý obraz reliktního vesmírného pozadí i s prvotními fluktuacemi, jež snad představují prvotní zárodky dnešních galaxií – viz následující obrázek 4.

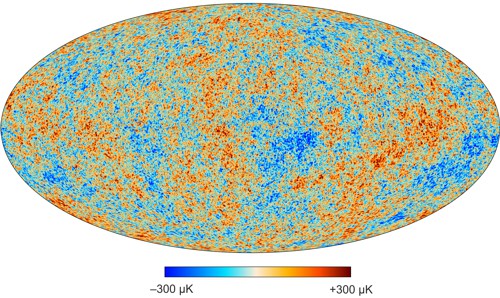
Obr. 4: Reliktní pozadí Vesmíru po odečtení dopplerovských
a dalších rušivých vlivů. Zdroj: Plack 2018.

Zajímavým aspektem těchto úvah je i fakt, že Einsteinovy rovnice produkují správný druh machovských vlivů, pouze pokud je ve vesmíru dostatek hmoty, aby se prostoročas gravitačně zakřivil „sám do sebe“. V otevřeném vesmíru, zasahujícím ve všech směrech do nekonečna, nelze rovnice žádným způsobem uvést do rovnováhy s konečným množstvím setrvačnosti. Obvykle to sloužilo jako argument proti tvrzení, že obecná teorie relativity zahrnuje Machův princip, protože se lidé domnívali, že vesmír nutně musí být otevřený. Nyní však máme dostatek přesvědčivých důkazů, že vesmír je ve skutečnosti uzavřený.

Astronomka Eleonora Di Valentino z britské Manchesterské univerzity a její kolegové s využitím dat evropské vesmírné observatoře PlanckPlanck – mikrovlnná observatoř evropské kosmické agentury ESA, která byla vynesena do vesmíru 14. května 2009. Byla určena k výzkumu fluktuací reliktního záření a monitorování vesmíru v mikrovlnné oblasti. Měla úhlovou rozlišovací schopnost 5′ a teplotní citlivost 2 μK. Oblohu snímkovala v devíti frekvenčních pásmech od 30 do 857 GHz (0,2 až 10 mm). Zrcadlo sondy mělo rozměry 1,9×1,5 m. Teplotu vysokofrekvenční části ohniska se podařilo po dobu dvou let udržet na extrémně nízké hodnotě 0,1 K. Činnost sondy byla ukončena v říjnu 2013. zveřejněných roku 2018 dokládají, že náš vesmír je zakřivený a uzavřený. Jejich výzkum uveřejnil časopis Nature Astronomy. Badatelé vyšli z principu gravitačních čoček. Ve své studii se přitom zaměřili právě na reliktní mikrovlnné záření pozadíReliktní záření – záření, které se od látky oddělilo přibližně 400 000 let po vzniku vesmíru, v době, kdy se vytvářely atomární obaly prvků a končilo plazmatické období vesmíru. Počáteční horkou (plazmatickou) fázi existence vesmíru nazýváme Velký třesk a reliktní záření tedy pochází z období konce Velkého třesku. Dnes má teplotu 2,73 K a vlnovou délku v milimetrové oblasti. Je jedním ze základních zdrojů informací pro naše poznání raného vesmíru. V anglické literatuře se označuje zkratkou CMB (Cosmic Microwave Background, mikrovlnné záření pozadí).. Z pozorování observatoře Planck a obzvláště z dat zveřejněných v roce 2018 plyne, že reliktní záření je gravitačně čočkováno silněji, než by podle stávajících modelů mělo být. Tým Planck Collaboration tomu říká anomálie Alens a doposud šlo o velkou záhadu. Podle týmu Di Valentino pro pozorovanou anomálii nabízí solidní fyzikální argumenty právě uzavřený vesmír.

Eleonora Di Valentino (*1986)



*  *  *

Všechny bulletiny této série

Odkazy