Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 6 – vyšlo 4. února, ročník 20 (2022) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

6/2022

Kvantování prostoročasu – paralelní světy

David Zoul

Při běžném pohledu se nám prostoročas jeví jako spojité hladké kontinuum, podobně, jako když se z vysoko letícího letadla díváme na povrch rozbouřeného oceánu. Vidíme pouze hladkou hladinu, jen mírně globálně zakřivenou do tvaru Zeměkoule. Seskočí-li pozorovatel padákem a postupně se blíží k hladině, vidí stále zřetelněji, že je rozvlněná. Když nakonec dopadne na hladinu, uvědomí si, jak daleko má hladina do ideálně rovné a hladké plochy. V metrových měřítcích silně fluktuuje místní zakřivení hladiny (vlny), v centimetrových a milimetrových měřítcích fluktuuje dokonce i topologickáTopologie – nauka o globálních vlastnostech a struktuře množin. Za topologicky ekvivalentní považujeme množiny, které lze spojitě deformovat jednu na druhou. Topologicky ekvivalentní nejsou množiny, lišící se přítomností „díry“, „slepením“ některých hraničních částí atd. Topologie vesmíru jako celku není známa. Rovnice obecné relativity nám umožňují jen sledování lokálních geometrických vlastností. struktura hladiny – oddělují se kapky, vznikají bubliny pěny.

Podobně v našem časoprostorovém „kontinuu“ čím menší mikrooblasti sledujeme, tím výrazněji se budou projevovat kvantové fluktuace geometrie, až nakonec v měřítcích Planckovy délkyPlanckovy škály – charakteristické rozměry získané kombinací fundamentálních konstant (gravitační, Planckovy a rychlosti světla). Planckova délka vychází 10⁻³⁵ m, Planckův čas 10⁻⁴³ s, Planckova hmotnost 10⁻⁸ kg a Planckova energie 10¹⁹ GeV. může silně fluktuovat i samotná topologie prostoru. Mohou se oddělovat nové „mikrovesmíry“, které vzápětí opět zanikají. U náhodně vzniklých dostatečně velkých fluktuací pak může dojít k jejich inflační expanziInflace – prudké (exponenciální) zvětšení rozměrů raného vesmíru. Zpravidla se dává do souvislosti s oddělením silné interakce v čase 10⁻³⁵ s od hypotetické nuly dané zpětnou extrapolací expanze. V průběhu inflace dojde k zvýšení entropie faktorem 10⁹⁰ až 10¹²⁰ a k zvětšení rozměrů faktorem 10³⁰ až 10⁵⁰. Uvolněná energie je minimálně 10⁶⁰ GeV, způsobí opětovné ohřátí vesmíru a vznik stochastických reliktních gravitačních vln. Některé modely kladou inflaci do ještě ranějších fází vývoje vesmíru. Pokud ale inflace existovala, je ona samotná skutečnou časovou nulou, skutečným počátkem našeho vesmíru. a vzniku nového „makrovesmíru“, jak jsme si vysvětlili v předchozím dílu (AB 3/2022).

Podle kvantové geometrodynamiky je tedy zdánlivě prázdné vakuum dějištěm nejbouřlivějších mikrojevů – prostoročas má jakousi „pěnovitou“ neustále spontánně fluktuující mikrostrukturu. Testovací částice budou v takovémto prostředí nemilosrdně zmítány, jako náš parašutista na rozbouřeném moři.

Obr. 1:Znázornění mikrofluktuací kvantového prostoročasu v dimenzionální redukciDimenzionální redukce – standardní matematická či fyzikální procedura aproximující určitý model tím, že se zaměříme pouze na určité vybrané stupně volnosti, zatímco všechny ostatní stupně volnosti ignorujeme. Například obtížně představitelnou pětirozměrnou varietu můžeme dimenzionální redukcí převést na matematicky snáze uchopitelný útvar s menším počtem dimenzí..
Zdroj: Peter Schreiber, Shutterstock.

Dimenzionální redukce – standardní matematická či fyzikální procedura aproximující určitý model tím, že se zaměříme pouze na určité vybrané stupně volnosti, zatímco všechny ostatní stupně volnosti ignorujeme. Například obtížně představitelnou pětirozměrnou varietu můžeme dimenzionální redukcí převést na matematicky snáze uchopitelný útvar s menším počtem dimenzí. Killingovo vektorové pole – zavádí se v diferenciální geometrii pro popis prostoročasových symetrií. Symetrie fyzikální soustavy je popisována lagranžiánem a vede k zákonům zachování určitých veličin (integrálů pohybu – především energie a hybnosti) i za použití křivočarých souřadnic a v zakřiveném prostoročase. Killingův vektor vyjadřuje složky nekonečně malé translace zachovávající délku (tzv. izometrie). Distribuce Killingova vektoru v každém bodě variety tvoří Killingovo vektorové pole infinitesimálních generátorů isometrií. Má-li prostoročas určité vlastnosti symetrie (např. sférickou, axiální nebo rovinnou) vyjádřené existencí příslušných Killingových vektorů, potom lze sestrojit vektor, pro který platí zákon zachování kovariantní hodnoty hybnosti, počítané v souřadnicové bázi. Podle toho, zda je Killingův vektor časového nebo prostorového typu, to lze interpretovat jako zákon zachování energie nebo hybnosti. Kalibrační bosony – kvanta kalibračních polí. Pokud potenciály pole rozšíříme přesně definovaným způsobem o libovolnou skalární funkci Q, pole si zachovají svoje vlastnosti nezávisle na volbě této funkce, neboli na tzv. kalibraci. Žádná měřitelná veličina totiž nesmí záviset na výběru té či oné kalibrace, a to ani v klasické, ani v kvantové mechanice – příroda je kalibračně invariantní. Přechod od jedné kalibrace k jiné nazýváme kalibrační transformací. Tato transformace často vyžaduje přítomnost nových kompenzujících polí, která nazýváme kalibračními poli, kvanta těchto polí pak kalibračními bosony. Doplňování symetrií do rovnic je základním principem teorií vystavěných na transformačních symetriích fyzikálních zákonů – tzv. kalibračních teorií. Vektorové bosony – kalibrační bosony se spinem rovným 1, u něhož funkce popisující jednotlivé projekce (−1, 0, 1) tvoří vektorové pole – odtud název. Zpravidla však tímto termínem označujeme pouze kvanta tří kalibračních polí slabé jaderné interakce, popsané grupou symetrií SU(2). Tyto částice označujeme symboly W+, W−, Z0. Objevili je Carlo Rubbia a Simon van der Meer v ženevské laboratoři CERN roku 1983, za což oba získali již o rok později Nobelovu cenu za fyziku.

Energie kvantového vakua

Sledujeme-li například magnetické pole o indukci B v prostorové oblasti charakterizované rozměrem l_h, bude tam obsažena energie pole úměrná B² l_h³ a čas potřebný ke změření pole bude l_h/c. Relace neurčitosti ΔE ?t ≳ h pak dává (ΔB)² l_h⁴ ≳ hc. Máme-li buňku o straně l_h a tedy ploše ~ l_h², budou zde kvantové fluktuace intenzity pole řádově

?B ≈ (hc)1/2 /lh2.

(1)

Hustota energie ~ hmoty pole v typické buňce dosahuje fantastických hodnot

ρ = (?B )2 / c2 = h/(clh4) ? 5×1096 kg/m3.

(2)

Tuto hustotu nazýváme Planckova-Wheelerova hustota hmoty, a je považována za mezní hodnotu koncentrace hmoty elektro­magne­tického či gravitačního záření v prostoročase. Charakteristická energie ~ hmota připadající na jednu buňku pak bude odpovídat Planckově hmotě M_h = 2,2×10⁻⁸ kg, tj. řádově 10²⁶ eV. To je o několik řádů více, než jsou největší energie částic zaznamenané doposud v kosmickém záření, a o 17 řádů více než klidové hmotnosti nejtěžších známých elementárních částic. Tyto obrovské hustoty jsou však evidentně v rozporu s velmi nízkou střední hustotou energie, kterou pozorujeme v současném vakuu. Vezmeme-li však úvahu příspěvek gravitace k hustotě energie a hmoty, pak dvě typické sousední buňky o hmotnostech m₁ ≈ m₂ ≈ M_h, jejichž středy jsou od sebe vzdálené l_h, budou mít při vzájemné gravitační interakci vazbovou energii

Egr = −Gm1m2 / r12 ? -c2/(hc/G)1/2.

(3)

Hmotový defekt dvou sousedních buněk

?mgr = Egr / c2 ? -(hc/G)1/2 = −Mh

(4)

je tedy záporný a stejného řádu jako kladná elektromagnetická hmotnost obou struktur. Může tedy lokálně kompenzovat energii příslušných fluktuací. Takto lokálně vykompenzované fluktuace již nevykazují gravitační přitažlivost s ostatními vzdálenějšími buňkami. Po takovéto celkové kompenzaci obrovských pikofluktuací může vakuum vypadat vskutku tak, jak jej pozorujeme.

Elementární částice, které však zřejmě nejsou zdaleka elementárními, jsou jakýmisi kolektivními excitacemi v moři zahrnujícím obrovské množství elementárních buněk, které se však všude jinde v průměru ruší, tvoříc v makroskopických měřítkách obvyklé vakuum.

Tím se podařilo odstranit jeden zapeklitý problém, který trápil fyziku již od 50. let minulého století, kdy byla formulována QEDQED – Quantum Electrodynamics, kvantová elektrodynamika, současná teorie elektromagnetické interakce. Teorie je postavená na Diracově rovnici pro elektron a na kvantové verzi teorie elektromagnetického pole. Polní částicí interakce je foton.. Přesto, že tato teorie předpovídá elektromagnetické jevy ve fantastické shodě s experimentem, právě její předpověď hustoty energie vakua se lišila od experimentálně stanovené hustoty energie vakua o plných 140 řádů, čímž se jednoznačně stala tou vůbec nejhorší předpovědí v dějinách fyziky.

Pětirozměrné unitární teorie

V letech 1921 až 1925 představili Theodor Kaluza a Oskat Klein zcela nový přístup k problému sjednocení gravitačního a elektro­magnetického pole. Pro obecný popis fyzikální reality navrhli používat pětirozměrnou varietu (v níž prostoročas OTRObecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách. je určitým čtyřrozměrným podprostorem) v naději, že pátý rozměr by mohl vyjadřovat elektromagnetické pole. Kaluza a Klein se zřejmě inspirovali způsobem, jakým Minkowski sjednotil v trojrozměrnu oddělené elektrické a magnetické pole přechodem ke čtyřrozměrnému prostoročasu.

Theodor Franz Eduard Kaluza (1885–1954), Oscar Benjamin Klein (1894–1977)

Fyzikální prostoročas pozorujeme jako čtyřrozměrný, takže „přebytečného“ pátého rozměru (který nemá přímý geometrický význam) je třeba se zbavit položením vhodné podmínky na pětirozměrnou geometrii. Kaluza původně zavedl poměrně umělý požadavek „cylindričnosti“, podle něhož v pětirozměrné varietě měla existovat jednorozměrná grupa izometrických transformací; vzniká tak Killingovo vektorové poleKillingovo vektorové pole – zavádí se v diferenciální geometrii pro popis prostoročasových symetrií. Symetrie fyzikální soustavy je popisována lagranžiánem a vede k zákonům zachování určitých veličin (integrálů pohybu – především energie a hybnosti) i za použití křivočarých souřadnic a v zakřiveném prostoročase. Killingův vektor vyjadřuje složky nekonečně malé translace zachovávající délku (tzv. izometrie). Distribuce Killingova vektoru v každém bodě variety tvoří Killingovo vektorové pole infinitesimálních generátorů isometrií. Má-li prostoročas určité vlastnosti symetrie (např. sférickou, axiální nebo rovinnou) vyjádřené existencí příslušných Killingových vektorů, potom lze sestrojit vektor, pro který platí zákon zachování kovariantní hodnoty hybnosti, počítané v souřadnicové bázi. Podle toho, zda je Killingův vektor časového nebo prostorového typu, to lze interpretovat jako zákon zachování energie nebo hybnosti., což vede k tomu, že pětirozměrná geometrická struktura může být plně popsána geometrií čtyřrozměrné hyperplochy. Později Einstein, Bergmann a Bargmann navrhli jinou geometrickou podmínku: uzavřenost (kompaktnost) pětirozměrné variety v pátém rozměru. Pětirozměrná varieta by pak měla topologickou strukturu M⁴×S¹, kde M⁴ je Minkowského prostoročas a S¹ je kružnice, tj. varieta by měla tvar tenké trubice. Pokud je poloměr této trubice (poloměr kompaktifikace) dostatečně malý (subatomárních rozměrů), nemůže se žádný makroskopický objekt v pátém rozměru pohybovat a prostoročas se efektivně jeví jako čtyřrozměrný.

Peter Gabriel Bergmann (1915–2002), Valentine Bargmann (1908–1989)

V teorii je bez újmy na obecnosti zvolena taková parametrizace metriky a označení veličin, aby se získaly Einsteinovy a Maxwellovy rovnice v obvyklém tvaru. Pátá proměnná pole – skalární veličina φ – je v Kaluzově-Kleinově teorii přebytečná a Kaluza ji vyloučil tím, že ji jednoduše položil rovnou jedné. Později byly činěny pokusy pochopit význam tohoto skalárního pole a dát mu kosmologický význam; Carl Brans a Robert Dicke dali toto pole do souvislosti se skalárním polem dalekého dosahu ve své tzv. skalárně-tenzorové teorii gravitace.

Carl Henry Brans (*1935), Robert Henry Dicke (1916–1997)

Einstein a Bergman chovali určitou dobu naději, že periodičnost polí vzhledem k páté zkompaktifikované souřadnici (podél níž by se pole mohla měnit s periodou rovnou délce kružnice kompaktifikace) by mohla vysvětlit kvantové jevy a umožnila vytvořit klasické modely elementárních částic. Tato podobnost s Bohrovým-Broglieovým kvantováním se však ukázala jen jako povrchní a příslušné naděje se neuskutečnily.

Kaluzova-Kleinova teorie nevedla ke kýženým výsledkům a na dlouhou dobu upadla prakticky v zapomnění. V posledních desetiletích však neočekávaně zažíváme „renesanci“ Kaluzovy-Kleinovy koncepce v souvislosti se snahami o geometrickou formulaci kvantové gravitace. Jedná se o zobecněné Kaluzovy-Kleinovy teorie, které poskytují zajímavé možnosti modelů vesmíru o vyšším počtu rozměrů.

Bránová kosmologie

Ve své nejjednodušší verzi tento termín v souvislosti s relativistickou kosmologií poukazuje na fyzikální obraz prostoročasu, v němž je náš čtyřrozměrný prostoročas časupodobnou nadplochou v pětirozměrném prostoročase M₅. Fyzikální hmota je omezená na náš vesmír M₄. V dimenzionální redukciDimenzionální redukce – standardní matematická či fyzikální procedura aproximující určitý model tím, že se zaměříme pouze na určité vybrané stupně volnosti, zatímco všechny ostatní stupně volnosti ignorujeme. Například obtížně představitelnou pětirozměrnou varietu můžeme dimenzionální redukcí převést na matematicky snáze uchopitelný útvar s menším počtem dimenzí., kde jsme schválně odebrali dvě prostorové dimenze, situaci znázorňuje obr. 2.

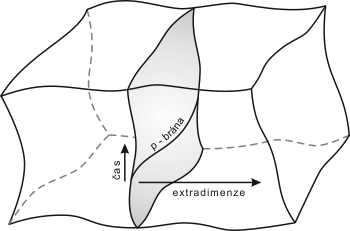
Obr. 2: Schematické znázornění 3-brány v pětirozměrném prostoročasu. S vývojem 3-brány v čase vzniká čtyřrozměrná nadplocha znázorněná šedou barvou.

Obecně p-bránou (coby zobecněním termínu „membrána“, kterým obvykle označujeme útvar dimenze 2) nazýváme p-dimenzionální prostorupodobnou podvarietu nějakého D-dimenzionálního (D > p + 1) prostoročasu M_D, který se nazývá prostor světů, či v angličtině krátce bulk. Toto je dosti obecná definice; dále se omezíme na fyzikálně opodstatněný případ, kdy dimenze prostoru světů je rovna D = p + 2. Souřadnice x^a (a = 1, … , p + 2) na prostoru světů sestávají z časové souřadnice t, prostorových souřadnic x^μ (μ = 1, … , p) na p-bráně a z jedné transverzální (tzv. extra) souřadnice z.

Samotný 3-rozměrný prostor je pak 3-bránou. V obecném D-rozměrném prostoročase může být obecně libovolný počet p-brán, z nichž alespoň jedna – náš vesmír – zahrnuje standardní model částicové fyziky coby dobře ověřenou teorii elementárních částic. Gravitace není omezena na p-brány, nýbrž naopak zprostředkovává interakce mezi nimi. Na rozdíl od ostatních sil není gravitace nikdy upoutána na bránu, neboť gravitony mohou nerušeně cestovat mezi jednotlivými bránami uvnitř vícerozměrného bulku.

Historicky prvním modelem bránového světa byl model Petra Hořavy a Edwarda Wittena, následovaný záhy modelem Arkani-Hameda, Dimopoulose a Dvaliho, kteří studovali (4+d)-dimenzionální plochý prostor světů, v němž d dimenzí má toroidální geometrii. Pozoruhodný pokrok poté přinesly práce Randallové a Sundruma. V nich byl nalezen zakřivený prostor světů tvořený řezem anti-de Sitterova (AdSVesmír AdS – Anti de Sitterův vesmír, maximálně symetrický vesmír s konstantní zápornou křivostí. Maximální symetrie znamená, že všechny body v tomto vesmíru jsou si rovnocenné. Záporná skalární křivost je způsobena zápornou hodnotou kosmologické konstanty. AdS vesmír se většinou uvažuje bez přítomnosti hmoty, která způsobuje kladné zakřivení prostoročasu. Tento prostoročas je pojmenován podle ředitele Leidenské observatoře, profesora Willema de Sittera.) prostoročasu.

Nima Arkani-Hamed (*1972), Savas Dimopoulos (*1952), Georgi (Gia) Dvali (*1964)

Hořavova – Wittenova teorie – sekvestrované brány

V modelu Petra Hořavy a Eda Wittena, prezentovaném roku 1996, obsahuje každá z brán různou sadu částic a sil. Sil a částic je na každé bráně dost na to, aby obsáhly celý standardní modelStandardní model – současný obecně přijímaný model částic a interakcí. Obsahuje kvarky, leptony, polní částice jednotlivých interakcí (fotony, gluony, W⁺,  W⁻, Z⁰) a Higgsovu částici jakožto zdroj hmotnosti ostatních částic a narušení symetrie elektroslabé interakce. Součástí modelu není gravitační interakce. Standardní model je vybudován na základě kvantové teorie pole., dokonce i jeho rozšířenou verzi v podobě grandunifikační teorie (GUTGUT – Grand Unified Theory, teorie velkého sjednocení. Popisuje sjednocení elektroslabé a silné interakce při energiích 10¹⁶ GeV (GUT škála). Při vyšších energiích než 10¹⁶ GeV existovaly pouze GUT interakce a gravitační interakce. Teorie velkého sjednocení předpovídá zatím nepozorované procesy, jako je například rozpad protonu.) a ještě něco navíc. Hořava a Witten předpokládali, že částice a síly standardního modelu „žijí“ na jedné bráně, zatímco další, dosud nepozorované částice předpovídané jejich teorií, „žijí“ na jiných bránách. Gravitace se pak pohybuje mezi bránami vícerozměrným bulkem. Jediný způsob, jak spolu mohou částice upoutané na různé brány komunikovat, je skrze částici, jež se může volně šířit bulkem. Tomuto jevu říkáme sekvestrace.

Petr Hořava (*1964). Zdroj: Martin Svozílek, Hospodářsdké noviny.

Myšlenka sekvestrace spočívá v oddělení částic zodpovědných za narušení symetrie od částic standardního modelu (či jeho rozšířené verze GUT). Částice sekvestrované na různých bránách spolu mohou interagovat jen velmi slabě prostřednictvím částic, jež se mohou šířit bulkem mezi jednotlivými bránami.

Arkani-Hamedova – Dimopoulosova osvětlená sekvestrace

Dlouhou dobu (od formulace standardního modelu na počátku 70. let minulého století) zůstávaly záhadou rozdílné hmotnosti různých vůníVůně – základní kvantová vlastnost leptonů a kvarků. Nejde o skutečnou vůni, ale o vlastnost, která vyjadřuje druh částice. Leptony mají šest vůní: elektron, elektronové neutrino, mion, mionové neutrino, tauon, tauonové neutrino. Kvarky mají také šest vůní: down (dolů), up (nahoru), strange (podivnost), charm (půvab), bottom (spodní), top (horní). kvarkůKvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce. a leptonůLeptony – skupina částic, mezi které patří elektron, těžký elektron (mion) a supertěžký elektron (tauon) a jejich neutrina (elektronové, mionové a tauo­nové). Tyto částice nepodléhají silné interakci, ale jen slabé a elektro­mag­ne­tické (pokud jsou nabité).. Standardní model předpokládá, že by hmotnosti těchto částic měly být určeny převážně hmotností virtuálních oblaků vektorových bosonůVektorové bosony – kalibrační bosony se spinem rovným 1, u něhož funkce popisující jednotlivé projekce (−1, 0, 1) tvoří vektorové pole – odtud název. Zpravidla však tímto termínem označujeme pouze kvanta tří kalibračních polí slabé jaderné interakce, popsané grupou symetrií SU(2). Tyto částice označujeme symboly W⁺, W⁻, Z⁰. Objevili je Carlo Rubbia a Simon van der Meer v ženevské laboratoři CERN roku 1983, za což oba získali již o rok později Nobelovu cenu za fyziku., jež je obklopují. Jak víme, hmotnost vektorovým bosonům uděluje Higgsův mechanismus. To však znamená, že síla interakce s Higgsovým bosonem musí být vůni od vůně velmi rozdílná, což představovalo velikou záhadu, neboť kalibrační interakce všech tří vůní částice jednoho typu (například kvarků u, c, t) jsou velmi podobné.

Nima Arkani-Hamed a Savas Dimopoulos se pokusili tento problém vyřešit předpokladem, že každá vůně interaguje s bulkovou částicí vycházející z jiné brány – brány, ležící pokaždé za jinak vzdálenou bránou. Narušení symetrie způsobené vzdálenějšími bránami by bylo menší než u brán bližších, podobně, jako klesá hodnota osvětlení se vzdáleností od světelného zdroje. Tato myšlenka proto dostala označení osvětlená sekvestrace.

Kaluzovy – Kleinovy módy

Kaluzovy – Kleinovy módy (částice) jsou průmětem vícerozměrné částice cestující bulkem do méněrozměrného prostoru. Pokud si například představíme náš třírozměrný prostor jako plochou bránu (tj. odmyslíme si jednu dimenzi), pak Kaluzova – Kleinova částice tvaru například duté kuličky by se při průletu naší bránou jevila jako drobný kroužek, jehož průměr by se nejprve zvětšoval a poté opět zmenšoval, jak by částice bránu opouštěla. Kaluzovy – Kleinovy (K-K) módy jsou tedy průmětem vícerozměrných částic do našeho čtyřrozměrného (tři prostorové rozměry a jeden časový) světa. Každá bulková částice, nesoucí vícerozměrnou hybnost, je v našem efektivním čtyřrozměrném světě nahrazena K-K módem, který však neobsahuje informaci o složkách hybnosti ve směru extradimenzí. Extradimenzionální hybnost K-K částic se nám proto musí prozrazovat jinak než běžná čtyřrozměrná hybnost. Podle vztahu mezi hmotností a hybností plynoucího ze speciální teorie relativity se nám bude extradimenzionální hybnost jevit jako klidová hmotnost.

K-K módy natažené mezi různými bránami mohou nabývat pouze diskrétních hodnot své energie. Jejich čtyřrozměrné obrazy by na naší bráně nabývaly posloupnosti různých hmotností. Čím vzdálenější brány spolu interagují, tím menší hmotnost K-K módů bychom měli naměřit.

Randallové – Sundrumovy (RS) modely

RS1 model

Obecná teorie relativity je konzistentní s tím, že energie a hybnost částic uvězněných na bránách zakřivuje prostoročas v pětirozměrném bulku a na gravitony v bulku to má zásadní dopad. Podrobný výpočet, který provedli Lisa Randall a Raman Sundrum v roce 1998 ukázal, že řešením Einsteinových rovnic pro uvažovaný případ je nám již dobře známý AdS prostoročasVesmír AdS – Anti de Sitterův vesmír, maximálně symetrický vesmír s konstantní zápornou křivostí. Maximální symetrie znamená, že všechny body v tomto vesmíru jsou si rovnocenné. Záporná skalární křivost je způsobena zápornou hodnotou kosmologické konstanty. AdS vesmír se většinou uvažuje bez přítomnosti hmoty, která způsobuje kladné zakřivení prostoročasu. Tento prostoročas je pojmenován podle ředitele Leidenské observatoře, profesora Willema de Sittera.. Ten má tu vlastnost, že libovolný řez, vedený v pětirozměrném bulku rovnoběžně s bránami, představuje opět zcela plochý prostor. Křivost se mění pouze ve směru kolmém na brány. Takový prostor označujeme výrazem pokřivený, na rozdíl od prostoru zakřiveného, v němž se geometrie mění ve všech prostorových směrech. Pokřivení prostoročasu mění celkovou škálu pro souřadnice místa, času, hmotnosti a energie v libovolném bodě pouze podél páté dimenze. Odráží se však rovněž v pravděpodobnostní funkci gravitonu podél páté dimenze.

Lisa Randall (*1962), Raman Sundrum (*1963)

Výsledkem je celkové přeškálování délek a času ve směru páté dimenze. Pravděpodobnostní funkce gravitonu udává, jak velká je pravděpodobnost nalezení gravitonu v daném místě prostoru, a tím i gravitační síla. Jelikož je v AdS prostoročasuVesmír AdS – Anti de Sitterův vesmír, maximálně symetrický vesmír s konstantní zápornou křivostí. Maximální symetrie znamená, že všechny body v tomto vesmíru jsou si rovnocenné. Záporná skalární křivost je způsobena zápornou hodnotou kosmologické konstanty. AdS vesmír se většinou uvažuje bez přítomnosti hmoty, která způsobuje kladné zakřivení prostoročasu. Tento prostoročas je pojmenován podle ředitele Leidenské observatoře, profesora Willema de Sittera. každý řez plochý, pravděpodobnostní funkce gravitonu je ve 4 prostoročasových dimenzích všude konstantní, a mění se pouze v páté dimenzi. Jakmile opustíme bránu s velkou kladnou energií, amplituda pravděpodobnosti gravitonu klesá exponenciálně směrem k sousední bráně, nesoucí nižší energii. V blízkosti druhé brány je tak gravitační interakce velmi slabá. Tato brána odpovídá našemu světu, v němž „bydlí“ standardní modelStandardní model – současný obecně přijímaný model částic a interakcí. Obsahuje kvarky, leptony, polní částice jednotlivých interakcí (fotony, gluony, W⁺,  W⁻, Z⁰) a Higgsovu částici jakožto zdroj hmotnosti ostatních částic a narušení symetrie elektroslabé interakce. Součástí modelu není gravitační interakce. Standardní model je vybudován na základě kvantové teorie pole..

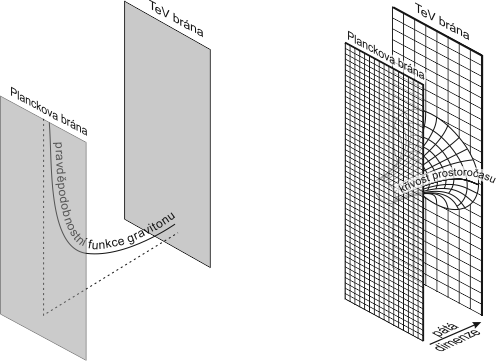
Obr. 3: Uvnitř bulku se amplituda pravděpodobnosti gravitonu, stejně jako rozměry,
hmotnosti a energie, exponenciálně mění podél páté dimenze.

Řešení problému kalibrační hierarchie

Položme si otázku, jak může síla gravitace nést informaci o tom, kde se objekt v páté dimenzi nachází. Rozuzlení spočívá ve skutečnosti, že gravitační přitažlivost závisí na hmotnosti a podél páté dimenze se spojitě mění. Jednou z mnoha pozoruhodných vlastností pokřiveného AdS prostoročasu je exponenciální pokles energie a hybnosti částic ve směru brány se zápornou energií. V duchu kvantové teorie poleKvantová teorie pole – popis interakce založený na kvantových principech, tj. na nekomutativnosti základních operací v mikrosvětě. Kvantová teorie pole nahrazuje silové působení polními částicemi. Tyto částice jsou virtuální a nikdy nemohou skončit v detektoru, působí jen mezi dvěma interagujícími částicemi. Jako první prototyp kvantové teorie pole se vyvinula ve 30. letech 20. století kvantová elektrodynamika, později se objevila teorie slabé a silné interakce. Jediná gravitace je popsána jinak – za pomoci obecné relativity. to pak znamená, že vzdálenosti a čas musí naopak v tomto směru expandovat, jak naznačuje obrázek 3 vpravo. Hmotnost a energie se v každém bodě podél páté dimenze přeškáluje úměrně amplitudě pravděpodobnostní funkce gravitonu. Ve směru páté dimenze tedy hmotnost a energie exponenciálně klesají.

Zatímco na jedné bráně sídlí částice zavlečené nepříjemnými vedlejšími efekty kvantové teorie poleKvantová teorie pole – popis interakce založený na kvantových principech, tj. na nekomutativnosti základních operací v mikrosvětě. Kvantová teorie pole nahrazuje silové působení polními částicemi. Tyto částice jsou virtuální a nikdy nemohou skončit v detektoru, působí jen mezi dvěma interagujícími částicemi. Jako první prototyp kvantové teorie pole se vyvinula ve 30. letech 20. století kvantová elektrodynamika, později se objevila teorie slabé a silné interakce. Jediná gravitace je popsána jinak – za pomoci obecné relativity., zmíněnými ve druhé části našeho seriálu, až k Planckovým energiím, na druhé bráně mohou být pouze v řádu teraelektronvoltůElektronvolt – jednotka energie. Jde o energii, kterou získá elektron urychlením v potenciálovém rozdílu jeden volt, 1 eV = 1,6×10⁻¹⁹ J. V jaderné fyzice se používají spíše větší násobky této jednotky, kiloelektronvolt keV (10³ eV), megaelektronvolt MeV (10⁶ eV), gigaelektronvolt GeV (10⁹ eV), teraelektronvolt TeV (10¹² eV) nebo petaelektronvolt PeV (10¹⁵ eV). V těchto jednotkách se také vyjadřuje hmotnost (E=mc²) a teplota (E=k_BT). Jeden elektronvolt odpovídá teplotě přibližně 11 600 K., tzn. o 16 řádů menší. V literatuře se proto vžilo označení Planckova brána a TeV brána, viz obr. 3. Hmotnost Higgsovy částiceHiggsovy částice – částice, které se objevují ve sjednocené teorii elektromagnetické a slabé interakce (tzv. elektroslabé interakce) standardního modelu. Částice a jim odpovídající Higgsovo pole zde zajišťují nenulovou hmotnost polních částic slabé interakce a způsobují narušení symetrie elektroslabé interakce při energiích nižších než 100 GeV. Částice jsou pojmenovány podle skotského fyzika Petera Higgse. Tento mechanizmus nazýváme Higgsův mechanizmus a je aplikovatelný i na jiné částice. Existence Higgsovy částice byla s největší pravděpodobností potvrzena v červenci 2012 na dvou detektorech urychlovače LHC v CERNu. O Higgsově částici se často hovoří jako o Higgsově bosonu, Higgsově poli či jen higgsi. tím automaticky přestává býti záhadou – jestliže žijeme na TeV bráně, pak jeho hmotnost v řádu desetin TeV nepřekvapí, ačkoli je o 17 řádů pod úrovní Planckovy hmoty. Je pozoruhodné, že k řešení problému kalibrační hierarchie ve skutečnosti stačí, aby na TeV bráně uvízla pouze Higgsova částice – kalibrační bosonyKalibrační bosony – kvanta kalibračních polí. Pokud potenciály pole rozšíříme přesně definovaným způsobem o libovolnou skalární funkci Q, pole si zachovají svoje vlastnosti nezávisle na volbě této funkce, neboli na tzv. kalibraci. Žádná měřitelná veličina totiž nesmí záviset na výběru té či oné kalibrace, a to ani v klasické, ani v kvantové mechanice – příroda je kalibračně invariantní. Přechod od jedné kalibrace k jiné nazýváme kalibrační transformací. Tato transformace často vyžaduje přítomnost nových kompenzujících polí, která nazýváme kalibračními poli, kvanta těchto polí pak kalibračními bosony. Doplňování symetrií do rovnic je základním principem teorií vystavěných na transformačních symetriích fyzikálních zákonů – tzv. kalibračních teorií. tomuto omezení podléhat nemusí. Higgsovo pole je totiž odpovědné za spontánní narušení symetrieSpontánní narušení symetrie – samovolná změna symetrie systému z vyšší symetrie na nižší při přechodu do nižšího energetického stavu. Typickým příkladem je narušení všesměrové symetrie při změně vody v led. Obdobně při ochlazování feromagnetického materiálu dojde při Curieově teplotě ke změně chování feromagnetika – vytvoří se Weissovy domény a naruší se původní symetrie. Spontánní narušení symetrie je důležitým jevem v částicové fyzice, například při energiích nižších než řádově 100 GeV dojde k rozdělení elektroslabé interakce na elektromagnetickou a slabou. a to je prapůvodem hmotností kalibračních bosonů a zprostředkovaně též kvarků a leptonů. Hmotnost kalibračních bosonů by byla nulová, pokud by Higgsovo pole kalibrační symetrii nenarušovalo. Energetická škála slabé interakceSlabá interakce – interakce s konečným dosahem, který je přibližně 10^–17 m. Působí pouze na levotočivé kvarky a leptony. Polními částicemi jsou vektorové bosony W⁺, W⁻ a Z⁰ se spinem rovným jedné. Hmotnosti částic jsou v rozmezí (80÷90) GeV. Typickým slabým procesem je například beta rozpad neutronu. Teorie slabé interakce se nazývá kvantová flavourdynamika (QFD). v řádu teraelektronvoltů bude chráněná, ale při velmi vysokých energiích srovnatelných dejme tomu s GUTGUT – Grand Unified Theory, teorie velkého sjednocení. Popisuje sjednocení elektroslabé a silné interakce při energiích 10¹⁶ GeV (GUT škála). Při vyšších energiích než 10¹⁶ GeV existovaly pouze GUT interakce a gravitační interakce. Teorie velkého sjednocení předpovídá zatím nepozorované procesy, jako je například rozpad protonu., může přesto dojít k dalšímu sjednocení sil.

RS2 model – lokalizovaná gravitace

V roce 1999 si Randallová a Sundrum uvědomili, že prostoročas může být ve směru páté dimenze pokřivený tak, že se gravitace zkoncentruje do blízkosti každé brány a toto soustředění může být tak výrazné, že se energie ostatních brán stane nepodstatnou. Jedná se ve skutečnosti o důsledek faktu, že gravitační pole působí i na samotné gravitony (i samo gravitační pole má hmotnost), který jsme zmínili již dříve. Kolmo ke zdrojové bráně tedy gravitační pole opět exponenciálně slábne, není to ale nikterak podmíněno existencí záporné energie sousední brány. Její celková energie může být klidně nulová, nebo sousední brána dokonce vůbec nemusí existovat.

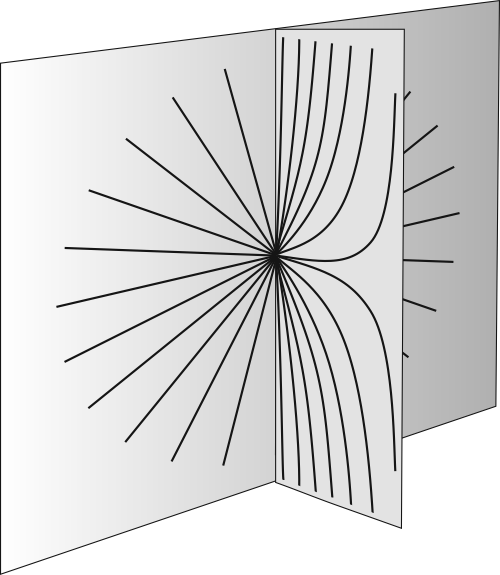
Obr. 4: V pokřiveném prostoru se gravitační siločáry podél brány šíří rovnoměrně všemi směry. Ve směru páté dimenze se však siločáry prudce ohýbají a ve vzdá­le­nosti jedné Planckovy délky od brány již pokračují prakticky rovnoběžně s bránou.

Prostorový přesah gravitačního pole mimo povrch brány směrem do páté dimenze je v tomto scénáři srovnatelný s rozměrem Planckovy délky. Přesněji řečeno, gravitace sice teoreticky zasahuje do nekonečna, její pokles se vzdáleností od brány je však tak rychlý, že se tato stává prakticky zanedbatelnou již na vzdálenosti jedné Planckovy délky. Bez ohledu na konečnost či nekonečnost páté dimenze se tato efektivně jeví, jako by měřila napříč pouze jednu Planckovu délku.

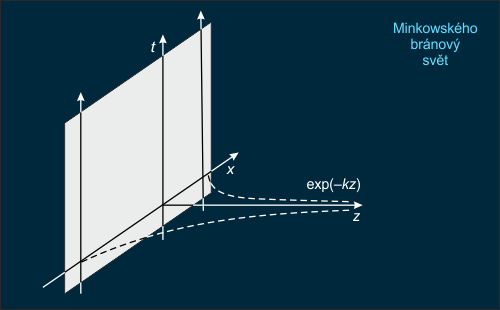
Obr. 5: Vnoření Minkowského bránového světa do 5-dimenzionálního
AdS v Poincarého souřadnicích

Kaluzovi – Kleinovi partneři

Když Randallová a Sundrum spočítali pravděpodobnostní funkce K-K partnerů gravitonu, zjistili, že tyto částice interagují na bránách přesně v souladu s předpovědí OTRObecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách. . První K-K částice na níž narazili, byla částice s nulovou klidovou hmotností (nulovou hybností ve směru páté dimenze) a spinem 2, jejíž pravděpodobnostní funkce je koncentrována na Planckově bráně a směrem od ní exponenciálně klesá. Jak již jistě tušíte, tento nehmotný K-K mód odpovídá čtyřrozměrnému gravitonu, který zprostředkuje běžnou gravitaci ve čtyřrozměrném prostoročase.

Další K-K módy se ale výrazně liší – pro každou hodnotu hmotnosti mezi nulou a Planckovou hmotou existuje odpovídající K-K částice o této hmotnosti a pravděpodobnostní funkce každé této částice má výrazné maximum na jiném místě podél páté dimenze. Jak jsme si uvedli v předešlých odstavcích, když cestujeme pryč od Planckovy brány, procházíme postupně místy, s nimiž je spojena exponenciálně klesající energie. Každému bodu ve směru páté dimenze lze přiřadit určitou hmotnost a tato hmotnost je spojena s Planckovou hmotností již zmíněným přeškálováním v tomto bodě. K-K částice, jejíž amplituda pravděpodobnosti má maximum v určitém bodě, nese právě takto přeškálovanou Planckovu hmotnost. Cestujeme-li podél páté dimenze směrem od Planckovy brány, potkáváme postupně K-K částice s maximem v oblasti, kde se právě nacházíme, a tyto částice jsou čím dál tím lehčí. Těžké K-K částice jsou vykázány z těch oblastí pětirozměrného prostoru, kde je přeškálovaná energie příliš malá, zatímco lehké částice naopak málokdy najdeme tam, kde se vyskytuje velké množství částic o mnohem vyšších energiích.

Hmotnosti částic standardního modelu

K-K módy jsou totožné s částicemi standardního modelu, až na to, že jejich hmotnosti odrážejí jejich hybnost v páté dimenzi, která je určena jejich polohou v bulku, jak jsme si uvedli v předešlém odstavci. Pro každou částici standardního modelu by tak mělo existovat mnoho K-K partnerů se stejnými hodnotami nábojů, ale různými hmotnostmi. Každý z těchto partnerů však žije na jiné světoploše ve směru páté dimenze.

Vraťme se nyní k předpokladu, jejž vyslovili Hamed a Dimopoulos (a ještě před nimi vlastně Juan Maldacena) a nechme různé vůněVůně – základní kvantová vlastnost leptonů a kvarků. Nejde o skutečnou vůni, ale o vlastnost, která vyjadřuje druh částice. Leptony mají šest vůní: elektron, elektronové neutrino, mion, mionové neutrino, tauon, tauonové neutrino. Kvarky mají také šest vůní: down (dolů), up (nahoru), strange (podivnost), charm (půvab), bottom (spodní), top (horní). částic standardního modeluStandardní model – současný obecně přijímaný model částic a interakcí. Obsahuje kvarky, leptony, polní částice jednotlivých interakcí (fotony, gluony, W⁺,  W⁻, Z⁰) a Higgsovu částici jakožto zdroj hmotnosti ostatních částic a narušení symetrie elektroslabé interakce. Součástí modelu není gravitační interakce. Standardní model je vybudován na základě kvantové teorie pole. interagovat s různými bránami podél páté dimenze. Budeme přitom předpokládat, že v každém bodě maxima některého z K-K módů leží jedna brána. Na průměru Planckovy délky tak máme bezpočet brán s exponencielně klesající energií částic.

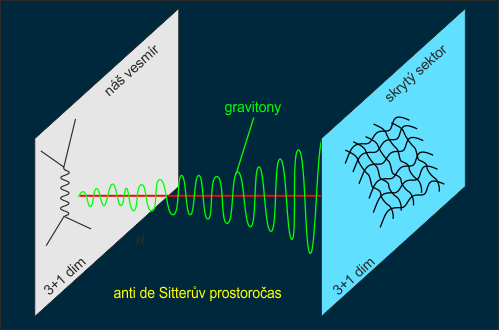
Obr. 6: Pokles energie K-K partnerů od jedné brány ke druhé

Na hraničních bránách v bulku je hmotnost částic standardního modelu zavlečena mechanizmem kalibrační hierarchie až k Planckově energii (viz druhý díl). Směrem k vnitřním bránám však energie K-K partnerů každé planckovské částice postupně klesá díky AdS pokřivení prostoročasu – viz obr 6. Pakliže je v bulku více brán, pak ke každé planckovské částici existuje na vnitřních bránách bulku bezpočet jejích K-K-partnerů o hmotnostech postupně klesajících směrem do středu bulku. Tato hmotnost je přitom určena vzdáleností brány, z níž daný K-K-partner pochází, neboť hmotnost každé další brány přispívá svým dílem k pokřivení prostoročasu uvnitř bulku. Jak hmotnost brán směrem do středu bulku postupně klesá, zmenšují se i jejich příspěvky k pokřivení AdS prostoročasu. Například K-K-partner elektronu pochází ze vzdálenější brány, než K-K-partner top kvarku. Proto se nám top kvark jeví výrazně hmotnějším, než je elektron – viz obr. 7.

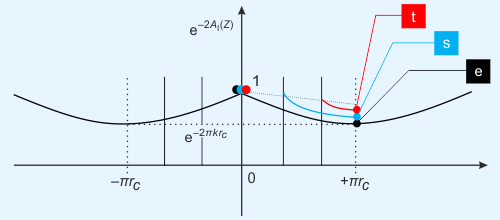
Obr. 7: Metrická funkce exp[−2A_I(Z)] pro Randallové-Sundrumův kompaktifikova­ný model typu I má periodický průběh s periodou sahající od bulku k bulku

Brány spolu mohou interagovat i vícečetně, takže jedna planckovská částice může mít na téže bráně i více K-K partnerů, pocházejících z interakce této brány s několika různě vzdálenými planckovskými bránami v bulku. Ačkoli má Higgsova částice– narušitel elektroslabé symetrie – energii pouhých 126 GeVElektronvolt – jednotka energie. Jde o energii, kterou získá elektron urychlením v potenciálovém rozdílu jeden volt, 1 eV = 1,6×10⁻¹⁹ J. V jaderné fyzice se používají spíše větší násobky této jednotky, kiloelektronvolt keV (10³ eV), megaelektronvolt MeV (10⁶ eV), gigaelektronvolt GeV (10⁹ eV), teraelektronvolt TeV (10¹² eV) nebo petaelektronvolt PeV (10¹⁵ eV). V těchto jednotkách se také vyjadřuje hmotnost (E=mc²) a teplota (E=k_BT). Jeden elektronvolt odpovídá teplotě přibližně 11 600 K., spojuje ji teorie s další částicí, na níž působí i silná interakce – s Higgsovým bosonem velkého sjednocení GUTGUT – Grand Unified Theory, teorie velkého sjednocení. Popisuje sjednocení elektroslabé a silné interakce při energiích 10¹⁶ GeV (GUT škála). Při vyšších energiích než 10¹⁶ GeV existovaly pouze GUT interakce a gravitační interakce. Teorie velkého sjednocení předpovídá zatím nepozorované procesy, jako je například rozpad protonu., o hmotnosti v řádu 10¹⁵ GeV. Máme zde tedy dvě částice propojené navzájem symetrií GUT, jejichž hmoty se vzájemně liší o 13 řádů. V teorii GUT musí tyto dvě Higgsovy částice působit společně, neboť silná interakce má být s interakcí elektroslabou za vysokých energií zaměnitelná, aby se obě síly staly srovnatelnými. Jsou-li silná a slabá interakce sjednoceny, pak každá částice citlivá na slabou interakci (včetně Higgsovy) musí mít partnera citlivého na silnou interakci. Tento partner Higgsova bosonu interaguje zároveň s kvarky i s leptony a dovoluje protonu se rozpadat.

Pokusme se vynést hmotnosti částic standardního modelu do grafu – na základě výše popsaného modelu očekáváme, že půjdou zhruba proložit exponenciálou (na rozdíl od původního Hamedova a Dimopoulosova modelu osvětlené sekvestrace, který předpovídal mocninný pokles s mocninou odpovídající dimenzi). Hmotnosti vektorových bosonůVektorové bosony – kalibrační bosony se spinem rovným 1, u něhož funkce popisující jednotlivé projekce (−1, 0, 1) tvoří vektorové pole – odtud název. Zpravidla však tímto termínem označujeme pouze kvanta tří kalibračních polí slabé jaderné interakce, popsané grupou symetrií SU(2). Tyto částice označujeme symboly W⁺, W⁻, Z⁰. Objevili je Carlo Rubbia a Simon van der Meer v ženevské laboratoři CERN roku 1983, za což oba získali již o rok později Nobelovu cenu za fyziku. jsou (jak jsme si již vysvětlili) určeny interakcí s Higgsovým bosonem (a jsou s jeho hmotností určitým způsobem spjaty – všimněme si, že se hmotnosti Higgsova a vektorových bosonů neliší o víc, než několik málo desítek procent, zatímco hmotnosti ostatních částic skáčou o celé řády).

částice	hmotnost (keV)
e	511
d	3000
u	4000
μ	105658
s	130000
c	1300000
τ	1777000
b	4300000
W	80000000
Z	91000000
H	126000000
t	173000000

Tab. 1: Hmotnosti základních částic v kiloelektronvoltech

Vyneseme-li hmotnosti částic standardního modelu do semilogaritmického grafu (viz graf 1), měly by jít zhruba proložit přímkou, která je obrazem exponenciály v semilogaritmickém souřadném systému. Výsledek je naprosto ohromující – na první pohled zcela náhodně vyhlížející hmotnosti částic standardního modelu najednou dávají dobrý smysl – oscilují okolo exponenciální funkce přesně tak, jak předpovídá výše popsaný bránový model.

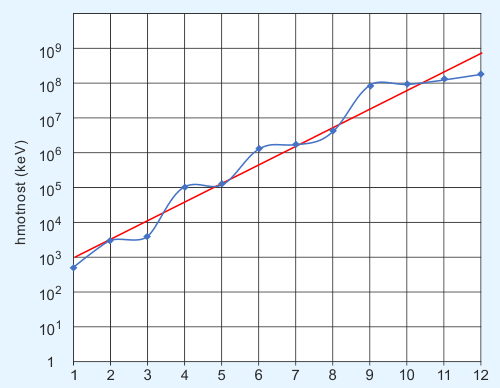
Graf 1: Průběh klidové hmotnosti základních částic

Ihned nás v grafu upoutá, že odchylky od přesné exponenciály mají jakýsi stupňovitý charakter. To naznačuje, že určité malé skupinky částic standardního modelu společně interagují s toutéž bránou. Tyto skupiny jsem v tabulce 1 vyznačil různými stupni šedi. Jedinci uvnitř skupin se liší svojí hmotností jen poměrně málo, a rozdíly lze vysvětlit drobnými odlišnostmi ve struktuře oblaků kalibračních bosonů, jež dle standardního modelu tvoří převážnou část hmoty každé z uvažovaných částic. Částice v každé skupině lze proto v prvním přiblížení nahradit jedinou myšlenou částicí, nesoucí hmotnost vypočtenou v prvním přiblížení jako aritmetický průměr hmotností všech částic skupiny a interagující tudíž se stejnou bránou, jako reálné částice skupiny. Výsledek je znázorněn grafem 2. O exponenciální závislosti nyní již nemůže býti nejmenších pochyb.

částice	hmotnost (keV)
elektron	511
1. skupina	3500
2. skupina	117829
3. skupina	2459000
4. skupina	117500000
interpolovaný mód	1690097170

Tab. 2: Průměrné klidové hmotnosti (keV) několika různých K-K módů

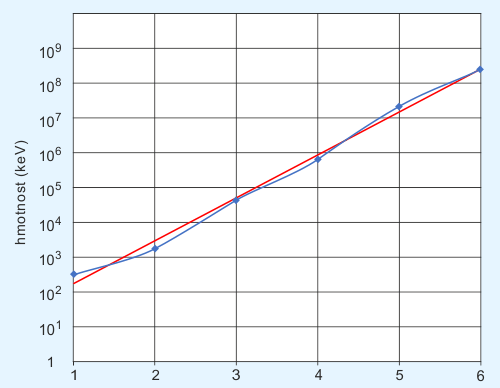
Graf 2: Exponenciální charakter klidové hmotnosti základních částic

Nalezli jsme tedy tvar funkce, jež potenciálně předpovídá hmotnosti částic. Interpolací z grafu 2 zjistíme, že další brána a tedy hmotnosti další skupiny částic, leží ve vzdálenosti možná jen jednoho až dvou TeV. Energie superurychlovače LHCLHC – Large Hadron Collider. Urychlovač protonů na nominální energie 14 TeV. LHC byl vybudován ve středisku jaderného výzkumu CERN v tunelu po urychlovači LEP II, který má obvod 27 km. Do zkušebního provozu byl uveden v září 2008, ale zanedlouho došlo k poruše na jednom z magnetů. Urychlovač byl opětovně spuštěn v listopadu 2009. Od března 2010 probíhal fyzikální program na energii 7 TeV. V roce 2012 byl na urychlovači objeven Higgsův boson. Provoz na energiích blízkých nominální probíhá od roku 2015. v ženevském středisku CERNCERN – Conseil Européen pour la Recherche Nucléaire, Evropské centrum jaderného výzkumu. Komplex urychlovačů a laboratoří na pomezí Švýcarska a Francie založený v roce 1954. Na výzkumu se podílí 22 členských zemí včetně České republiky. K největším objevům patří detekce polních částic slabé interakce, příprava antivodíku a vytvoření kvarkového-gluonového plazmatu, pralátky, z níž vznikal vesmír. V současné době je zde vybudován největší urychlovač světa – Large Hadron Collider, který byl po závadě na jednom z magnetů opětovně spuštěn na konci roku 2009. V roce 2012 byl na LHC objeven Higgsův boson, poslední částice standardního modelu. V CERNu byl také vynalezen a poprvé použit Web. by na pozorování částic této skupiny měla poměrně hladce dosáhnout a předpovězené částice v průběhu času detekovat.

Maldacenova dualita opět na scéně

Ve čtvrtém dílu jsme zmínili pozoruhodnou vlastnost AdS prostoruVesmír AdS – Anti de Sitterův vesmír, maximálně symetrický vesmír s konstantní zápornou křivostí. Maximální symetrie znamená, že všechny body v tomto vesmíru jsou si rovnocenné. Záporná skalární křivost je způsobena zápornou hodnotou kosmologické konstanty. AdS vesmír se většinou uvažuje bez přítomnosti hmoty, která způsobuje kladné zakřivení prostoročasu. Tento prostoročas je pojmenován podle ředitele Leidenské observatoře, profesora Willema de Sittera., jíž je existence duální čtyřrozměrné teorie. Juan Maldacena objevil explicitní příklad této duality, když si všiml, že vše, co se děje v pětirozměrném AdS prostoročase, lze popsat v rámci duální konstrukce, která funguje ve čtyřrozměrném prostoročase, v němž panují extrémně silné interakce se speciálními vlastnostmi. Pětirozměrný AdS prostor s gravitací, ale bez brán, je ekvivalentní čtyřrozměrné teorii bez gravitace. Jakmile ale do pětirozměrné teorie vložíme brány, duální čtyřrozměrná teorie se rázem obohatí právě o gravitaci.

Ukázali jsme, že objekt, cestující podél páté dimenze, by se ve čtyřrozměrném světě zvětšoval, nebo zmenšoval. Ve třetím dílu jsme viděli, že čtyřrozměrný plochý a jednoduše souvislý vesmír je duální pětirozměrné zakřivené geometrii s toroidální topologickou strukturou. Jednotlivé brány jsou v této topologiiTopologie – nauka o globálních vlastnostech a struktuře množin. Za topologicky ekvivalentní považujeme množiny, které lze spojitě deformovat jednu na druhou. Topologicky ekvivalentní nejsou množiny, lišící se přítomností „díry“, „slepením“ některých hraničních částí atd. Topologie vesmíru jako celku není známa. Rovnice obecné relativity nám umožňují jen sledování lokálních geometrických vlastností. reprezentovány oddělenými toroidálními soustřednými vrstvami, jejichž malý výřez znázorňuje obr. 8. Z obrázku je vcelku zřejmá nutnost natahování, či naopak smršťování dimenzí během cestování bulkem mezi jednotlivými soustřednými toroidálními bránami. Uvědomíme-li si, že každá brána musí obsahovat tentýž počet elementárních Planc­kových buněk (na obr. 8 s odečtenou jednou dimenzí tedy každá soustředná plocha obsahuje stejný počet elementárních Planc­kových plošek), pak tyto buňky se na různých bránách z pětirozměrného pohledu musí jevit různě veliké. Jelikož je ale Planckova buňka základním invariantem a měřítkem velikosti v prostoru, musel by každý objekt, jenž by chtěl přecestovat z jedné brány na jinou, upravit svoji velikost podmínkám panujícím na cílové bráně tak, aby počet jeho Planckových objemů zůstal zachován, viz obr. 1 čvrtého dílu.

Obr. 8: Prostoročasové čtyřbrány v pětirozměrné duální teorii se efektivně chovají
jako série soustředných toroidů uvnitř toroidů. Zdroj: YT/Nueva Teoría del Todo.

Hypergrupy

V dimenzionální redukciDimenzionální redukce – standardní matematická či fyzikální procedura aproximující určitý model tím, že se zaměříme pouze na určité vybrané stupně volnosti, zatímco všechny ostatní stupně volnosti ignorujeme. Například obtížně představitelnou pětirozměrnou varietu můžeme dimenzionální redukcí převést na matematicky snáze uchopitelný útvar s menším počtem dimenzí., kterou jsme si zjednodušili náš 4D prostoročas na dvourozměrnou toroidální plochu si lze celou záležitost představit poměrně snadno. Lze si ale představit pětirozměrný prostor světů, popsaný v tomto dílu, bez dimenzionální redukce? V prostoru světů bez dimenzionální redukce ztrácí pojem p-dimenzionálních membrán (p-brán) svůj názorný smysl. Namísto něj používáme termín hypergrupa.

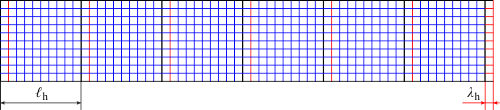
Obr. 9: Hypergrupy

Pro první seznámení s tímto pojmem se na chvíli ještě uchýlíme k dimenzionální redukci, tentokrát jen o jednu prostorovou dimenzi. Na obrázku 9 jsou dvourozměrné analogie buněk prostoru vyznačeny černě. Všechny buňky patřící do tzv. naší hypergrupy (označme si ji například symbolem α) jsem černě orámoval. Buňky, jež jsou vůči naší hypergrupě posunuty o vektor ϑ, pro jehož velikost platí

ϑ = k λh,

(5)

kde k ∈ {1, 2, … , l_h/ λ_h – 1}, tvoří cizí hypergrupu – paralelní svět. Číslo ϑ nazýváme hypergrupární bariérou mezi dvěma různými hypergrupami, čili interhypergrupární bariérou. Jak se jeví celá situace ve 3D-pohledu ukazuje obrázek 10. Uvažujeme-li vzájemnou translaci hypergrup pouze po horizontálách a vertikále tak, jak je to naznačeno v předchozím výkladu, potom v našem nejbližším okolí dostáváme celkem 6 přilehlých hypergrup. Pokud uvážíme ještě translaci po rovinných diagonálách, přidá se k těmto šesti blízkým hypergrupám dalších 8 (viz obr. 11 nalevo). Provedeme-li translaci hypergrup po prostorových diagonálách, jak naznačuje obrázek 11 napravo, získáme navíc 8 hypergrup v naší těsné blízkosti.

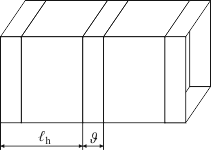
Obr. 10: Lineární interhypergrupární translace

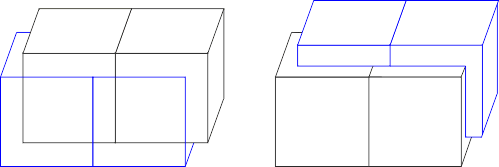
Obr. 11: Planární (nalevo) a prostorová (napravo) interhypergrupární translace

Celkem tak máme 22 hypergrup které jsou od té naší odděleny tou nejtenčí možnou interhypergrupární bariérou. V prostoru tak může obrazně řečeno běžet paralelně více programů naráz. Situaci lze připodobnit k případu, kdy máme doma k jednomu počítači připojeno více monitorů. Mohli bychom pak sledovat na každém z těchto monitorů do značné míry nezávislý průběh každého jednoho z běžících programů. Právě takový jeden program zobrazený na jednom z monitorů představuje v naší analogii hypergrupy α 



*  *  *

Všechny bulletiny této série

Odkazy