Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie.
Vydavatel: AGA (Aldebaran Group for Astrophysics)
Číslo 19 – vyšlo 10. května, ročník 22 (2024)
© Copyright Aldebaran Group for Astrophysics
Publikování nebo šíření obsahu je zakázáno.
ISSN: 1214-1674,
Email: bulletin@aldebaran.cz

Slupkový model

Adam Prášek

V několika bulletinech (AB 18/2023, 29/2023, 15/2024) jsme se zmínili o tom, že slupkový modelSlupkový model jádra – popisuje jádro jako soubor vzájemně interagujících nukleonů. Kvantové stavy jádra jsou kombinací stavů jednotlivých nukleonů, které získáme řešení Schrödingerovy rovnice. Skupiny stavů s podobnou hodnotou energie tvoří slupky, někdy však může vlivem silné spin-orbitální interakce docházet k překryvu jejich energií. je analogií elektronů obsazujících hladiny v atomovém obalu. Pojďme se proto podívat na jeho konstrukci detailněji. Protony a neutrony jsou vázané systémy tří elementárních částic – kvarkůKvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce.. Jelikož je vazebná energie protonu či neutronu mnohem vyšší než vazebná energie jádra, lze kvarkovou strukturu zanedbat a uvažovat jen jako elementární částice. Přesto se vyskytují situace, kdy je třeba podniknout cestu do samotného nitra částic, z nichž se atomové jádro skládá, abychom porozuměli jeho struktuře.

Umělecká představa atomu s atomovým jádrem

Umělecká představa atomu s elektrony a atomovým jádrem uprostřed.
Zdroj: Institute of Modern Physics, Chinese Academy of Sciences.

Atom – základní strukturní jednotka hmoty, jádro je složeno z neutronů a protonů, obaly z elektronů. Rozměry atomu jsou 10⁻¹⁰ m, rozměry jádra 10⁻¹⁴ m, hustota atomu je 10¹¹ g·cm⁻³, hustota jádra 10¹⁴ g·cm⁻³. Elektrony nejsou v atomárnáím obalu lokalizovány, můžeme určit jen pravděpodobnosti jejich výskytu v tzv. orbitalech.

Slupkový model jádra – popisuje jádro jako soubor vzájemně interagujících nukleonů. Kvantové stavy jádra jsou kombinací stavů jednotlivých nukleonů, které získáme řešení Schrödingerovy rovnice. Skupiny stavů s podobnou hodnotou energie tvoří slupky, někdy však může vlivem silné spin-orbitální interakce docházet k překryvu jejich energií.

Kapkový model jádra – jádro je popisováno na základě analogie s kapkou kapaliny o poloměru přibližně R = 1,2×A^1/3 fm. V rámci tohoto jednoduchého modelu dokážeme přibližně určit střední vazbovou energii na jeden nukleon pomocí semiempirické Weizsackerovy formule.

Silná interakce

Silná interakceSilná interakce – interakce krátkého dosahu, přibližně 10⁻¹⁵ m. Silná interakce je výběrová, působí jen na částice s barevným nábojem, tj. kvarky. Polními částicemi silné interakce jsou gluony (z anglického „glue“ = lepit, lepidlo). Gluony spojují kvarky do větších celků, tzv. hadronů. Nejznámější jsou proton a neutron složený ze tří kvarků. Silná interakce je odpovědná za soudržnost atomárního jádra. Polní částice mají barevný náboj a proto mohou působit samy na sebe. Barevný náboj na malých vzdálenostech (při vysokých energiích) slábne a kvarky se chovají jako volné částice. Hovoříme o tzv. asymptotické volnosti kvarků. Teorií silné interakce se nazývá kvantová chromodynamika (QCD). působí jen mezi kvarkyKvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce. a gluonyGluony – intermediální (polní, výměnné) částice silné interakce, která působí na hadrony a je krátkého dosahu. Tato interakce spojuje kvarky v mezony a baryony, udržuje pohromadě neutrony a protony v atomovém jádře a způsobuje některé rychlé rozpady elementárních částic. Celkem známe 8 gluonů. Tyto polní částice jsou nositeli barevného náboje (náboje silného interakce). Tím se silná interakce odlišuje od elektromagnetické a slabé interakce. a je dána barevným nábojem částic – ten je analogií elektrického náboje u elektromagnetické interakceElektromagnetická interakce – interakce působící na všechny částice s elektrickým nábojem. Má nekonečný dosah, mezi tělesy ubývá s druhou mocninou vzdálenosti. Polními částicemi jsou fotony, které vytvářejí mezi nabitými tělesy elektromagnetické pole. Nemají elektrický náboj, mají nulovou klidovou hmotnost a spin rovný jedné. Teorie elektromagnetické interakce se nazývá kvantová elektrodynamika (QED).. Specifickou vlastností silné interakce je tzv. barevné uvěznění, kdy vázaná částice složená z kvarků má vždy neutrální barevný náboj. Situace je podobná tomu, jako když elektrony v atomu obsazují elektronové orbitaly tak, aby byl atom jako celek neutrální, ovšem je zde jeden rozdíl – zatímco atom lze snadno ionizovat, tak ionizační energie kvarků je natolik vysoká, že při pokusu o uvolnění kvarku vytvoříme kvarky nové, a namísto rozštěpení například mezonu dostaneme mezony dva. Důvodem, proč silná interakce působí i mezi částicemi s neutrálním barevným nábojem, jako jsou nukleonyNukleon – společný název pro částice jádra (protony a neutrony). Jde o baryony složené z kvarků „u“ a „d“., je to, že ačkoli má proton či neutron neutrální barevný náboj, tak jsou kvarky v jeho nitru rozloženy nehomogenně – vznikají momenty barevného náboje, které jsou nenulové. Opět se jedná o situaci analogickou s elektromagnetickou interakcí – vodík s jedním elektronem je elektricky neutrální, ale protože je zde náboj rozložen nehomogenně, bude mít nenulový elektrický dipólový moment.

Interakci mezi nukleony neboli reziduální silnou interakci, lze tedy chápat jako interakci způsobenou barevným momentem a můžeme ji popsat jako výměnu polní částice, podobně jako je tomu ve standardním modeluStandardní model – současný obecně přijímaný model částic a interakcí. Obsahuje kvarky, leptony, polní částice jednotlivých interakcí (fotony, gluony, W⁺, W⁻, Z⁰) a Higgsovu částici jakožto zdroj hmotnosti ostatních částic a narušení symetrie elektroslabé interakce. Součástí modelu není gravitační interakce. Standardní model je vybudován na základě kvantové teorie pole., tentokrát ale roli polních částic zastávají mezonyMezon – částice složená z jednoho kvarku a jednoho antikvarku. Název vznikl z toho, že první objevené mezony měly hmotnost „mezi“ hmotností elektronu a protonu. Pokud se kvarky složí s nesouhlasným spinem, vznikne skalární mezon (má nulový spin), pokud se souhlasným spinem vznikne vektorový mezon (spin má roven jedné). Skalární mezony zkombinované z kvarků „d“ a „u“ nazýváme piony, vektorové róony. Pokud mezon obsahuje kvark „s“, nazývá se kaon..

Schéma silné interakce. Vidíme, že nukleon-nukleonová interakce, základní vstup
do modelů jaderné struktury, není vůbec jednoduchá. Zdroj: Wikipedia.

Barevný moment a potenciál

Interakci způsobenou barevným momentem lze charakterizovat pomocí potenciálu mezi dvěma nukleony, který lze využít při studiu struktury jader ve slupkovém modelu. Tento potenciál má velmi silnou odpudivou část a lokální minimum na vzdálenosti asi 0,8 fm. Pro výpočet struktury jader se příliš nehodí – silná odpudivá část způsobuje problémy se stabilitou výpočtů a navíc se ukazuje, že potenciál působící v jádře se chová jinak – jeho profil je ovlivněn přítomností ostatních nukleonů.

Z těchto důvodů se zavádí efektivní potenciál. V haló jádrechHaló jádra – zvláštní skupina jader s neobvyklou vnitřní stavbou. Na většinu z nich můžeme nahlížet jako na systém sestávající ze dvou složek: z jadérka a z haló tvořeného jedním nebo více slabě vázanými valenčními nukleony. U normálního jádra je jeho poloměr úměrný třetí odmocnině z počtu jeho nukleonů. Tato jednoduchá závislost ale u haló jader neplatí. Oblast, ve které se mohou slabě vázané valenční nukleony vyskytnout, odpovídá jádrům s daleko větším nukleonovým číslem. (viz AB 32/2023) je střední vzdálenost mezi nukleony větší než dosah interakce. Ve slupkovém modelu často pracujeme s ještě podivnější představou – interakce má dosah nulový. Může to znít nesmyslně, ale je třeba si uvědomit, že nukleony nemají přesně určenou polohu – jádro ve skutečnosti není pouhou soustavou kuliček, lepší je představit si ho jako soubor jakýchsi polí, jejichž hodnota v daném bodě určuje pravděpodobnost, že v tomto bodě částici nalezneme. To znamená, že interakce je dána pravděpodobností, že v daném místě budou obě částice. To vede k myšlence zavést potenciál úměrný jaderné hustotě, což odpovídá představě, že nukleon interaguje jen s nukleony v nejbližším okolí.

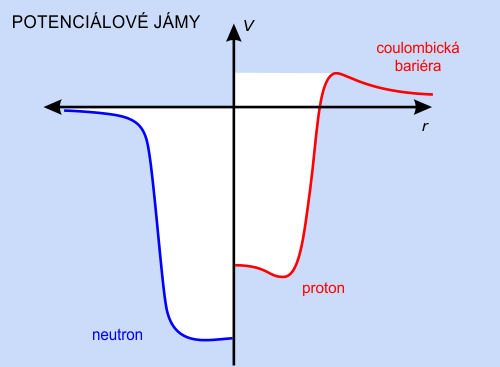
Woodův-Saxonův potenciál je vhodnou aproximací interakce mezi nukleony. Tento potenciál je úměrný hustotě jádra – modrá křivka pro neutrony pak odpovídá záporně vzaté hustotě jádra. Pro protony vidíme deformovaný tvar potenciálu, což je dáno kombinací jaderné a elektromagnetické interakce. Zdroj: Stockholms universitet.

Poznamenejme, že výše uvedený potenciál je navržen pro aproximaci středním polem, tj. namísto systému mnoha interagujících nukleonů uvažujeme interakci se středním polem, které charakterizuje vliv ostatních nukleonů. Tato představa sice vypadá velmi hrubě, ale jedná se o jednu z mála metod, jak zkoumat strukturu těžkých jader. Aproximaci středním polem se dostává v teorii jaderné struktury značné pozornosti a existuje řada přístupů, jak do něj zahrnout nejrůznější interakce částic – tuto metodu označujeme jako Hartreeho-Fockovu metodu, případně Hartreeho-Fockovu-Bogoljubovu metodu pro zahrnutí párové interakce.

Různé přístupy ke slupkovému modelu

Někteří autoři nazývají slupkovým modelem situaci, kdy máme soubor nukleonů vzájemně interagujících prostřednictvím určité interakce, a hledají pro tuto interakci odpovídající řešení, viz např. [3]. Naopak v [2] je jako slupkový model uvažována situace, kdy se nukleony pohybují v nějakém efektivním poli, které nahrazuje působení ostatních nukleonů. V takto pojatém slupkovém modelu jádra se nukleony pohybují v určitém středním poli, které je parametrem úlohy. Koncepce je analogická pohybu elektronů v poli jádra. Rozdíl je v tom, že jaderný potenciál je kombinací jaderné interakce a elektromagnetické interakce a že není příliš znám jeho tvar. Ten je totiž dán právě strukturou jádra, kterou se ale snažíme modelovat. Tento zamotaný kruh řeší právě Hartreeho-Fockova metoda, jejíž princip je takový, že odhadneme potenciál například z experimentální hustoty jádra, a poté použijeme výsledky k dopočtení potenciálu, s nímž provedeme nový, korigovaný výpočet. Opakováním tohoto postupu lze dosáhnout velice kvalitních výsledků. Detaily postupu nechme na odborné literatuře, pro začátečníky se znalostmi kvantové teorie lze doporučit publikaci [2], pro pokročilejší zájemce o hlubší vhled do podstaty modelů publikaci [3].

Strukturu jádra atomu modelujeme podobně jako elektrony v atomárním obalu, které obsazují jednotlivé orbitalyOrbital – oblast v atomárním či molekulárním obalu, kde se vyskytuje elektron. Pravděpodobnost výskytu elektronu v orbitalu je rovna druhé mocnině velikosti komplexní vlnové funkce.. To je dáno tím, že se jedná o fermionyFermiony – částice, které mají poločíselný spin, vlnová funkce je antisymetrická, splňují Pauliho vylučovací princip a podléhají Fermiho–Diracovu statistickému rozdělení. Patří mezi ně všechny leptony, kvarky a baryony – například elektron, neutrino, proton a neutron. Při nízkých teplotách fermiony obsazují stavy postupně, až po tzv. Fermiho mez., které musejí splňovat Pauliho vylučovací principPauliho vylučovací princip – „Dva fermiony nemohou být nikdy ve stejném kvantovém stavu“. Právě proto různé elektrony v atomárním obalu zaujímají různé kvantové stavy a tím vytvářejí různorodé chování chemických prvků. – žádné dva elektrony nemohou být ve stejném kvantovém stavu, tj. nemohou mít stejná všechna kvantová čísla (hlavní kvantové čísloKvantové číslo, hlavní – značíme n, čísluje energii systému E_n. Hodnota energie závisí na průběhu potenciální energie. Energie je proto jinak kvantována ve vodíkovém atomu, jinak v harmonickém oscilátoru, kvantové jámě, atd. určující energii orbitalu, vedlejší kvantové čísloKvantové číslo, vedlejší – značíme l, vyjadřuje maximální možnou projekci momentu hybnosti do nějaké osy v jednotkách redukované Planckovy konstanty. U atomu vodíku nabývá vedlejší kvantové číslo hodnot 0, 1, ... n–1. Časté je označování vedlejšího kvantového čísla písmeny s, p, d, f..., které odpovídají hodnotám 0, 1, 2, 3... Velikost momentu hybnosti (nikoli projekce) je dána vztahem L² = l(l+1)ħ². určující moment hybnosti atd.). Naprosto stejná situace je i v jádrech – protony a neutrony obsazují své vlastní slupky, analogicky jako elektrony v elektronových orbitalech. Jediný podstatnější rozdíl spočívá v takzvané spin-orbitální interakciLS vazba – spin-orbitální interakce. Každý objekt má orbitální (l) a spinový (s) moment hybnosti. V kvantové teorii se oba momenty skládají do výsledného momentu hybnosti, který je charakterizován kvantovým číslem j nabývajícím hodnot od |l−s| do |l+s|.. SpinSpin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole. je veličina, která se podobá momentu hybnosti částic. Jedná se o jakousi vnitřní vlastnost částice. Pro nukleony má hodnotu ½, a projekce může nabývat buď ½, nebo –½. Spin-orbitální interakce pak odpovídá interakci spinu s momentem hybnosti. Pro elektrony je tento efekt slabý, ale pro nukleony v jádře je zcela zásadní a nelze jej zanedbat.

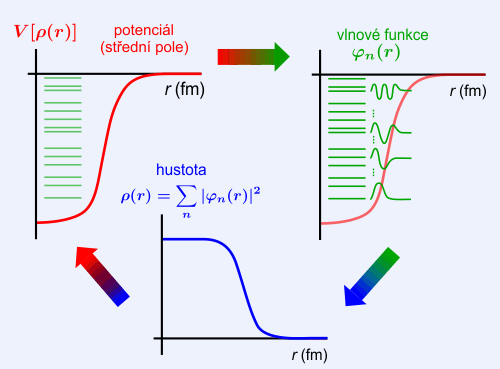
Princip výpočtu parametrů jádra ve slupkovém modelu – z potenciálu spočteme vlnové funkce a energie nukleonů, z těch se určí jaderná hustota a z hustoty určíme potenciál, z něhož se vypočítají nové energie a vlnové funkce. Pokud tento postup funguje, hovoříme o vnitřně konzistentním modelu středního pole. Zdroj: Wikimedia.

* * *

Slupkový model atomového jádra je přesnější alternativou ke kapkovému modelu už od 30. let 20. století, kdy v roce 1932 jeho první variantu navrhli Dmitrij Dmitrijevič Ivaněnko a Evgenij Nikitič Gapon. V roce 1949 model nezávisle zformulovali a detailněji analyzovali Marie Goeppert Mayerová a Hans Jensen, kteří za tuto práci obdrželi Nobelovu cenu za fyziku v roce 1963. Slupkový model je v mnoha situacích velmi úspěšným a někdy i jediným popisem chování atomového jádra.

Odkazy