Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 17 – vyšlo 29. dubna, ročník 20 (2022) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

17/2022

Mohou stroje nabýt vědomí?

David Zoul

Kvantová teorie informace

Pro elementární množství klasické informace, které získáme výběrem ze dvou hodnot 0, 1, zavedl Claude Shanon označení jeden bit coby zkratku anglického termínu binary digit. Fyzikální realizace bitu si žádá systém, se dvěma dobře definovanými stavy – například logický obvod bez napětí a s napětím. Roku 1995 zavádí Benjamin Schumacher element kvantové informace nazývaný qubit.

Umělecké ztvárnění stavebních jednotek kvantového internetu
vyvíjeného v Insbrucku. Zdroj: IQOQI, Harald Ritsch.

Qubit – kvantová verze bitu neboli kvantový bit, základní jednotka informace podléhající kvantové logice. Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Element kvantové informace zavedl Benjamin Schumacher roku 1995. Na qubit lze také pohlížet jako na virtuální částici a v analogii k antičásticím lze zavést rovněž antiqubit nesoucí zápornou informaci. Kvantová teleportace – děj navržený v roce 1993 Charlesem Bennettem a poprvé uskutečněný v roce 1997 v Innsbrucku Anthony Zeilingerem. Je založena na tenzorovém součinu Hilbertových prostorů (popisuje provázání – entanglement – stavů) a vzájemném vztahu různých bází (Bellovy stavy). Při kvantové teleportaci se přenášejí virtuální EPR (Einsteinovy-Podolského-Rosenovy) páry tzv. ebitů, vytvořené z entropického vakua. Konkrétní informační proces pak lze popsat pomocí analogie Feynmanových diagramů s ebity a antiebity. V reálných teleportačních obvodech pro kvantové počítače může hrát úlohu ebitu například spin elektronu obsazujícího orbitální stav v polovodičové kvantové tečce (spintronika). Hilbertův prostor – úplný lineární vektorový prostor se skalárním součinem. V kvantové teorii odpovídá každý kvantový stav paprsku v Hilbertově prostoru (všem nenulovým násobkům nějakého prvku). Lineární kombinace prvků odpovídají superpozici stavů. Vlastnosti Hilbertova prostoru umožňují hovořit o změnách stavu systému v geometrických pojmech, jako jsou projekce, rotace, zrcadlení apod. Feynmanovy diagramy – grafické zkratky pro jednotlivé části členů poruchové řady při řešení rovnic kvantové teorie pole. Tyto zkratky lze interpretovat jako elementární procesy interakce kvarků, leptonů a polních částic. Každému Feynmanovu diagramu odpovídá konkrétní matematický výraz a pro sestavování diagramů platí jednoduchá pravidla: počet vrcholů diagramu odpovídá pořadí v příslušné poruchové řadě a amplituda pravděpodobnosti dějů s každým dalším vrcholem klesá v poměru 1/137, který nazýváme konstanta jemné struktury. Linie částic, spojující jednotlivé uzly diagramu, nazýváme propagátory diagramu. Pouze propagátory s volnými konci představují skutečné částice, které lze registrovat v našich přístrojích. Propagátory, které začínají a končí ve vrcholu, odpovídají tzv. virtuálním částicím, které nerespektují zákon zachování energie. Tyto částice nikdy nemůžeme pozorovat (nemají volné konce linií). Jde například o polní částice zprostředkující sílu mezi skutečnými částicemi. BEC – Boseho-Einsteinův kondenzát (Bose Einstein Condensate, BEC), představuje stav hmoty, ve kterém jsou všechny částice v jednom jediném kvantovém stavu. Vlnové funkce se vzájemně překrývají a při fázovém přechodu vznikne společná vlnová funkce. Soustava částic se začne chovat jako jediná „superčástice“. Boseova-Einsteinova kondenzace vzniká u bosonů, které se mohou nacházet všechny v nejnižším energetickém stavu. Na rozdíl od běžné kondenzace, jako je tomu u fázových přechodů plynů na pevné látky, jde o kondenzaci v prostoru hybností. Přechod od klasického stavu ke kvantovému je náhlý, až dramatický. Kvantové chování se projevuje při teplotě nižší, než je tzv. teplota degenerace. Unitární transformace – změna stavu kvantového systému, která odpovídá rotaci nebo zrcadlení v Hilbertově prostoru.

Kvantová provázanost (entanglement)

Při přechodu ke kvantovým systémům se využívají opět dvoustavové systémy, jejichž stavy však můžeme popsat jako body ve dvoudimenzionálním Hilbertově prostoru (elektron se spinem nahoru a dolů, foton s polarizací horizontální a vertikální, atom v základním a excitovaném stavu apod.). Pak je přirozené hodnotám 0, 1 pro klasický bit přiřadit bázické stavy | 0 ⟩, | 1 ⟩. Jelikož v kvantové mechanice platí princip superpozice, může se kvantový bitQubit – kvantová verze bitu neboli kvantový bit, základní jednotka informace podléhající kvantové logice. Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Element kvantové informace zavedl Benjamin Schumacher roku 1995. Na qubit lze také pohlížet jako na virtuální částici a v analogii k antičásticím lze zavést rovněž antiqubit nesoucí zápornou informaci. nalézat zároveň v obou těchto stavech, což je výrazný rozdíl oproti klasické teorii informace, kde systém zaujímá vždy pouze jediný z možných stavů 0, nebo 1. Je vcelku pozoruhodné, že si tohoto významného rozdílu povšiml teprve v roce 1995 Ben Schumacher.

David Hilbert (1862–1943), Benjamin Schumacher (*1959)

Jeden kvantový bit (qubitQubit – kvantová verze bitu neboli kvantový bit, základní jednotka informace podléhající kvantové logice. Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Element kvantové informace zavedl Benjamin Schumacher roku 1995. Na qubit lze také pohlížet jako na virtuální částici a v analogii k antičásticím lze zavést rovněž antiqubit nesoucí zápornou informaci.) je pak definován formulí

\[|{\rm{qubit}}\;\rangle \equiv |\psi \;\rangle = \alpha |0\;\rangle + \beta |1\;\rangle \]

(1)

kde α a β jsou komplexní čísla taková, že |α|² + |β|² = 1 (jedná se o amplitudy pravděpodobnosti realizace jednotlivých stavů | 0 ⟩, | 1 ⟩). Dvojice čísel 0 a 1 umožňuje zakódovat informaci, jejíž množství by bylo podle klasické teorie informace jeden bitbit – základní jednotka klasické informace, která nabývá dvou hodnot (ano/ne), (0/1), (pravda/nepravda) atd. Násobnou jednotkou je kilobit označující 2¹⁰ = 1024 možností. Termín zavedl Claude Elwood Shanon coby zkratku anglického termínu binary digit. Fyzikální realizace bitu si žádá systém se dvěma dobře definovanými stavy – například logický obvod bez napětí a s napětím.. Dvouhladinový kvantový systém popsaný rovnicí (1) umožňuje tímto způsobem zakódovat množství kvantové informace. Často se jako qubit označuje samotný dvoustavový systém, jehož kvantový stav je popsán vektorem ve dvourozměrném Hilbertově prostoru.

I když qubit reprezentuje kontinuum možných stavů, v jediném qubitu je zakódován jediný klasický bit, neboť informaci lze získat pouze měřením, při kterém vlnová funkce (1) zkolabuje do jednoho z možných stavů – qubit se promítne do jednoho ze dvou možných bázových stavů. Vzhledem k tomu, že měření ovlivňuje měřený stav (dojde k tzv. dekoherenci), není možno uskutečnit měření postupně v různých bázích. Jinými slovy, při konkrétním měření kolabuje qubit s prav­dě­po­dobností |α|² do stavu | 0 ⟩ a s prav­dě­po­dobností |β|² do stavu | 1 ⟩.

Položme si nyní otázku, jak to bude vypadat v systémech s více než jedním qubitem. Předpokládejme opět, že systém bude tvořen elementy, které mohou nabývat dvou hodnot. V klasickém případě jsou pak možné stavy systému s n takových elementů repre­zentovány jako body v 2n-dimenzionálním vektorovém prostoru.

V kvantovém systému je odpovídající stavový prostor mnohem větší. Systém složený z n qubitů je reprezentován v 2ⁿ-dimenzionálním komplexním qubitQubit – kvantová verze bitu neboli kvantový bit, základní jednotka informace podléhající kvantové logice. Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Element kvantové informace zavedl Benjamin Schumacher roku 1995. Na qubit lze také pohlížet jako na virtuální částici a v analogii k antičásticím lze zavést rovněž antiqubit nesoucí zápornou informaci. Hilbertově prostoru. Tento základní rozdíl tkví v tom, že v případě klasického systému se jednotlivé stavové prostory n elementů kombinují jako kartézský součin, avšak kvantové stavy se kombinují jako tenzorový součin. Toto je základní fakt, který dovoluje exponenciálně urychlit výpočty na kvantových počítačích, oproti počítačům klasickým.

Uvažujme pro jednoduchost systém složený ze dvou qubitů. Označme H₁, H₂ dvoudimenzionální komplexní vektorové prostory s bázemi \(\left\{ {{v_1},{v_2}} \right\}\), \(\left\{ {{w_1},{w_2}} \right\}\). V klasickém případě může jako společná báze posloužit kartézský součin těchto dvou bází:

\[\left\{ {{v_1},{v_2}} \right\} \times \left\{ {{w_1},{w_2}} \right\} = \left\{ {{v_1},{v_2},{w_1},{w_2}} \right\}.\]

(2)

V kvantovém případě však musíme uvažovat tenzorový součin \(V \otimes W\), který má bázi

\[\left\{ {{v_1},{v_2}} \right\} \otimes \left\{ {{w_1},{w_2}} \right\} = \left\{ {{v_1} \otimes {w_1},{v_1} \otimes {w_2},{v_2} \otimes {w_1},{v_2} \otimes {w_2}} \right\}.\]

(3)

V konkrétním případě dvou qubitů, každý v bázi \(\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\}\) je hledanou bází

\[\left\{ {\left| 0 \right\rangle \otimes \left| 0 \right\rangle ,\left| 0 \right\rangle \otimes \left| 1 \right\rangle ,\left| 1 \right\rangle \otimes \left| 0 \right\rangle ,\left| 1 \right\rangle \otimes \left| 1 \right\rangle } \right\},\]

(4)

která se dá přepsat do tvaru

\[\left\{ {\left| {00} \right\rangle ,\left| {01} \right\rangle ,\left| {10} \right\rangle ,\left| {11} \right\rangle } \right\},\]

(5)

což by zpětně odpovídalo kódování klasických stavů 00, 01, 10, 11. Výše uvedený přepis znamená použití binárního kódu, tj. obecně

\[\left| x \right\rangle = \left| {{b_n},{b_{n - 1}},\; \ldots \;,{b_0}} \right\rangle ,\]

(6)

kde b_i jsou binární číslice 0, 1 pro rozvoj v binárním kódu. Jinými slovy, stavy systému dvou qubitů představují vektory ve čtyř­dimen­zionálním Hilbertově prostoru s bázovými vektory (5). Analogicky pro n = 3 qubity by to byla báze 2³ = 8 bázových vektorů ve tvaru

\[\begin{array}{c} \left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \otimes \left\{ {\left| {00} \right\rangle ,\left| {01} \right\rangle ,\left| {10} \right\rangle ,\left| {11} \right\rangle } \right\} = \\ = \left\{ {\left| {000} \right\rangle ,\left| {001} \right\rangle ,\left| {010} \right\rangle ,\left| {011} \right\rangle ,\left| {100} \right\rangle ,\left| {101} \right\rangle ,\left| {110} \right\rangle ,\left| {111} \right\rangle } \right\}. \end{array}\]

(7)

Vraťme se však k systému dvou qubitů. Podle principu superpozice se mohou realizovat například stavy

\[\alpha \left| {00} \right\rangle \pm \beta \left| {11} \right\rangle .\]

(8)

Ukážeme, že takové stavy nelze faktorizovat na stavy původních elementů – qubitů. Kdyby tomu tak bylo, pak by existovaly \({\alpha _1},{\alpha _2},{\beta _1},{\beta _2}\) takové, že

\[\begin{array}{c} \left( {{\alpha _1}\left| 0 \right\rangle + {\beta _1}\left| 1 \right\rangle } \right) \otimes \left( {{\alpha _2}\left| 0 \right\rangle + {\beta _2}\left| 1 \right\rangle } \right) = \\ = {\alpha _1}{\alpha _2}\left| {00} \right\rangle + {\alpha _1}{\beta _2}\left| {01} \right\rangle + {\beta _1}{\alpha _2}\left| {10} \right\rangle + {\beta _1}{\beta _2}\left| {11} \right\rangle = \alpha \left| {00} \right\rangle + \beta \left| {11} \right\rangle . \end{array}\]

(9)

Odtud je okamžitě vidět, že

\[\begin{array}{l} {\alpha _1}{\beta _2} = {\beta _1}{\alpha _2} = 0,\\ \alpha = {\alpha _1}{\alpha _2},\\ \beta = {\beta _1}{\beta _2}. \end{array}\]

(10)

To ovšem znamená, že

\[{\alpha _1}{\beta _2} = 0\quad \Leftrightarrow \quad {\alpha _1}{\alpha _2} = 0\quad \vee \quad {\beta _1}{\beta _2} = 0{\kern 1pt} .\]

(11)

Proto se takové stavy nazývají entanglované (vzájemně provázanéProvázaný stav – entanglement, kvantově korelovaný stav systému dvou a více částic, v němž nemá smysl mluvit o stavech jednotlivých složek. Například z provázaného stavu dvojice fotonů nelze vyjádřit stavy jednotlivých fotonů. Značíme |AB>+|XY>, což znamená, že najdeme-li první částici ve stavu A, je druhá ve stavu B. Je-li první ve stavu X, pak druhá je ve stavu Y. Měřením provedeným na jedné částici se dozvíme určitou informaci o částici druhé. Je to způsobeno tím, že mají společnou minulost. Někdy se také hovoří o propletených stavech. či propletené). Pro takové stavy zavedl Charles H. Bennett roku 1996 jednotku ebit (entanglovaný bit), která určuje míru entanglovanosti maximálně entanglovaného páru qubitů. Entanglement (kvantové provázání stavů) je čistě kvantovou vlastností, nemající klasickou analogii.

Charles Henry Bennett (*1943)

Kvantová teleportace

Kvantovou teleportací rozumíme přenos kvantové informace s následnou rekonstrukcí stavu kvantového systému na jiném místě. U kvantového systému není obecně možné získat úplnou informaci o teleportovaném systému – brání tomu princip neurčitosti. Navíc, při měření dochází k průmětu stavového vektoru na vlastní vektor a ke kolapsu vlnové funkce. V kvantové mechanice není možné klonovat čisté stavy, tj. vytvořit přesnou kopii kvantového systému. Přesto bylo dokázáno, že s využitím tenzorového součinu Hilbertových prostorů, což fyzikálně odpovídá využití entanglementu, je kvantová teleportace prakticky proveditelná.

Již v roce 1935 upozornili Einstein, Podolsky a Rosen (EPR) na existenci stavů dvoučásticových systémů, které mají v důsledku zákonů zachování tu vlastnost, že měření zvolené proměnné jedné částice úplně, a navíc okamžitě určuje výsledek měření odpovídající proměnné u druhé částice, nezávisle na její vzdálenosti. Uvažovaná proměnná druhé částice má přitom přesnou hodnotu bez ohledu na to, zda tato proměnná je u druhé částice skutečně měřena, či nikoliv. Bohr a Schrödinger ve své reakci zdůraznili, že entanglement dvou částic je nutno považovat za jediný kvantový systém. Částice s nulovým spinem (například pionPion – mezon π, částice s nulovým spinem složená z kvarků u a d. ) se rozpadne na dvě částice se spinem 1/2 (elektron a pozitron). Takto vzniklé částice se od sebe vzdalují a po čase provedeme měření spinu u první částice ve svislém směru. Naměříme-li projekci spinu do tohoto směru jako +1/2 (tzv. spin nahoru), musí být spin druhé částice −1/2 (tzv. spin dolů), aby byla zachována původní nulová hodnota celkového spinu. Kvantový stav systému částic 1 a 2 je potom součinem stavů jednotlivých částic, tj.

\[{\left| \uparrow \right\rangle _1}{\left| \downarrow \right\rangle _2}.\]

(12)

Se stejnou pravděpodobností jsme však mohli u částice 1 naměřit spin dolů a u částice 2 spin nahoru, tj.

\[{\left| \downarrow \right\rangle _1}{\left| \uparrow \right\rangle _2}.\]

(13)

Obecně je tedy kvantový stav systému částic 1 a 2 lineární kombinací (superpozicí) obou uvedených alternativ

\[\left| \psi \right\rangle = \frac{1}{{\sqrt 2 }}\left( {{{\left| \uparrow \right\rangle }_1}{{\left| \downarrow \right\rangle }_2} - {{\left| \downarrow \right\rangle }_1}{{\left| \uparrow \right\rangle }_2}} \right),\]

(14)

kde znaménko minus zajišťuje požadovanou nulovou hodnotu celkového spinu. Použitím spinových funkcí můžeme rovnost (14) přepsat na obvyklejší tvar

\[\left| \psi \right\rangle = \frac{1}{{\sqrt 2 }}\left( {{{\left| \phi \right\rangle }_1}{{\left| \chi \right\rangle }_2} - {{\left| \chi \right\rangle }_1}{{\left| \phi \right\rangle }_2}} \right),\]

(15)

odkud je opět zřejmé, že vlnová funkce entanglovaného stavu není faktorizovatelná – nelze ji vyjádřit jako součin činitelů, z nichž každý odpovídá jen jedné částici z uvažovaného EPR páru. Víme jen, že obě částice jsou v antikorelovaných stavech. Rovněž vidíme, že měření, jež vede u první částice k redukci stavového vektoru do stavu \(\left| \phi \right\rangle \), vede současně u druhé částice k redukci stavového vektoru do stavu  \(\left| \chi \right\rangle \) a naopak.

Kvantový stav dvojice dvoustavových systémů je reprezentován stavovým vektorem ve čtyřrozměrném Hilbertově prostoru. V něm lze za normální bázi zvolit Bellovy stavy

\[\begin{array}{l} {\left| {{\psi ^ + }} \right\rangle _{12}} = \frac{1}{{\sqrt 2 }}\left( {{{\left| H \right\rangle }_1}{{\left| V \right\rangle }_2} + {{\left| V \right\rangle }_1}{{\left| H \right\rangle }_2}} \right),\\ {\left| {{\psi ^ - }} \right\rangle _{12}} = \frac{1}{{\sqrt 2 }}\left( {{{\left| H \right\rangle }_1}{{\left| V \right\rangle }_2} - {{\left| V \right\rangle }_1}{{\left| H \right\rangle }_2}} \right),\\ {\left| {{\phi ^ + }} \right\rangle _{12}} = \frac{1}{{\sqrt 2 }}\left( {{{\left| H \right\rangle }_1}{{\left| H \right\rangle }_2} + {{\left| V \right\rangle }_1}{{\left| V \right\rangle }_2}} \right),\\ {\left| {{\phi ^ - }} \right\rangle _{12}} = \frac{1}{{\sqrt 2 }}\left( {{{\left| H \right\rangle }_1}{{\left| H \right\rangle }_2} - {{\left| V \right\rangle }_1}{{\left| V \right\rangle }_2}} \right), \end{array}\]

(16)

kde H respektive V jsme nyní označili horizontální, respekltive vertikální polarizaci fotonu. Výsledkem měření Bellových stavů je projekce stavového vektoru sledovaného systému částic 1 a 2 do jednoho ze čtyř uvedených Bellových stavů.

Obecné schéma kvantové teleportace

Teoretické schéma kvantové teleportace navrhl Bennett a kolektiv v roce 1993. Odesilatelka s již tradičním jménem Alice má částici 1 ve stavu \({\left| \psi \right\rangle _1}\), který v principu sice nezná, ale má o něm předat informaci rovněž již tradičně pojmenovanému příjemci Bobovi. Využije k tomu jednu ze dvou částic EPR páru, označenou číslem 2. Provede měření Bellových stavů na systému částic 1 a 2, jehož výsledkem je projekce stavového vektoru tohoto systému do jednoho ze čtyř uvedených Bellových stavů. Alice tím získá informaci o tom, který ze čtyř možných stavů (16) je pozorován, ale původní stav částice 1 tím zničí. Druhá částice z EPR páru, označená jako 3, se dostane k Bobovi. Alice mu klasickým spojovacím kanálem sdělí výsledek měření Bellových stavů. Bob pak může provést jednu ze čtyř možných unitárních transformací kvantového stavu částice 3. Tím rekonstruuje původní neznámý kvantový stav \({\left| \psi \right\rangle _1}\) částice 1. Bob obdrží kvantovou informaci okamžitě, díky nelokalitě kvantové korelace v EPR páru, avšak informace od Alice se šíří klasickým kanálem, a tedy nemůže překročit rychlost světla ve vakuu. Kvantová teleportace tak nenarušuje lorentzovskou invarianci prostoročasu. Kombinací klasického a kvantového způsobu přenosu informace však Bob získá přesnou repliku částice 1 v původním kvantovém stavu \({\left| \psi \right\rangle _1}\).

Uvedený obecný postup kvantové teleportace nyní popíšeme v konkrétnější podobě na jednoduchém příkladu teleportace polarizačního stavu fotonu, který označíme za částici 1. Může být polarizován horizontálně (H), nebo vertikálně (V), jedná se tedy o dvoustavový kvantový systém. Podle rovnice (1) je kvantový stav tohoto fotonu reprezentován stavovým vektorem

\[{\left| \psi \right\rangle _1} = \alpha {\left| H \right\rangle _1} + \beta {\left| V \right\rangle _1},\quad \quad {\rm{ }}{\left| \alpha \right|^2} + {\left| \beta \right|^2} = 1,\]

(17)

kde veličiny \({\left| \alpha \right|^2}\) resp. \({\left| \beta \right|^2}\) udávají pravděpodobnost, že u fotonu 1 bude naměřen polarizační stav \({\left| H \right\rangle _1}\) resp. \({\left| V \right\rangle _1}\). Alice nyní provede měření Bellových stavů na dvojici částic 1 a 2, přičemž částice 2 a 3 tvoří EPR entanglovaný pár, popsaný dle rovnice (15) stavovým vektorem

\[{\left| {{\psi ^ - }} \right\rangle _{23}} = \frac{1}{{\sqrt 2 }}\left( {{{\left| H \right\rangle }_2}{{\left| V \right\rangle }_3} - {{\left| V \right\rangle }_2}{{\left| H \right\rangle }_3}} \right).\]

(18)

Nechť je výsledkem tohoto měření například

\[{\left| {{\psi ^ - }} \right\rangle _{12}} = \frac{1}{{\sqrt 2 }}\left( {{{\left| H \right\rangle }_1}{{\left| V \right\rangle }_2} - {{\left| V \right\rangle }_1}{{\left| H \right\rangle }_2}} \right).\]

(19)

V tomto případě se kvantový stav částice 3 realizuje (díky jejímu entanglementu s částicí 2) ve tvaru identickém s částicí 1, neboli

\[{\left| \psi \right\rangle _3} = \alpha {\left| H \right\rangle _3} + \beta {\left| V \right\rangle _3}.\]

(20)

V případě výsledku (19) tedy může Alice Bobovi sdělit klasickým kanálem, že žádná další operace s částicí 3 již není potřeba. Původní kvantový stav částice 1 byl již úspěšně teleportován na částici 3. Pokud totiž byl při měření Bellových stavů pozorován stav \({\left| {{\psi ^ - }} \right\rangle _{12}}\), jsou podle rovnice (19) stavové vektory částic 1 a 2 korelované. Avšak podle rovnice (18) jsou také stavové vektory částic 2 a 3 vzájemně korelované, jak plyne z předchozího odstavce. Kvantový stav \({\left| \psi \right\rangle _{123}}\) systému všech tří částic před měřením Bellových stavů je totiž tenzorovým součinem \({\left| \psi \right\rangle _1}{\left| {{\psi ^ - }} \right\rangle _{23}}\), takže podle rovnic (17) a (18) je

\[\begin{array}{c} {\left| \psi \right\rangle _{123}} = {\left| \psi \right\rangle _1}{\left| {{\psi ^ - }} \right\rangle _{23}} = \frac{\alpha }{{\sqrt 2 }}\left( {{{\left| H \right\rangle }_1}{{\left| H \right\rangle }_2}{{\left| V \right\rangle }_3} - {{\left| H \right\rangle }_1}{{\left| V \right\rangle }_2}{{\left| H \right\rangle }_3}} \right) + \\ + \frac{\beta }{{\sqrt 2 }}\left( {{{\left| V \right\rangle }_1}{{\left| H \right\rangle }_2}{{\left| V \right\rangle }_3} - {{\left| V \right\rangle }_1}{{\left| V \right\rangle }_2}{{\left| H \right\rangle }_3}} \right), \end{array}\]

(21)

kde tenzorové součiny \({\left| {\;\;} \right\rangle _1}{\left| {\;\;} \right\rangle _2}\) lze vyjádřit pomocí levých stran v soustavě ( 16 ). Vztah ( 21 ) má potom tvar

\[\begin{array}{c} {\left| \psi \right\rangle _{123}} = \frac{1}{2}\left[ {{{\left| {{\psi ^ + }} \right\rangle }_{12}}\left( { - \alpha {{\left| H \right\rangle }_3} + \beta {{\left| V \right\rangle }_3}} \right) + {{\left| {{\psi ^ - }} \right\rangle }_{12}}\left( { - \alpha {{\left| H \right\rangle }_3} - \beta {{\left| V \right\rangle }_3}} \right) + } \right.\\ {\rm{ + }}\left. {{{\left| {{\phi ^ + }} \right\rangle }_{12}}\left( {\alpha {{\left| V \right\rangle }_3} - \beta {{\left| H \right\rangle }_3}} \right) + {{\left| {{\phi ^ - }} \right\rangle }_{12}}\left( {\alpha {{\left| V \right\rangle }_3} + \beta {{\left| H \right\rangle }_3}} \right)} \right]. \end{array}\]

(22)

Po měření Bellových stavů zůstává nenulovým právě jeden ze čtyř vektorů \({\left| {{\psi ^ \pm }} \right\rangle _{12}},{\left| {{\phi ^ \pm }} \right\rangle _{12}}\). Kulatá závorka v (22), která násobí tento nenulový bázový stav, popisuje stavový vektor částice 3, tj. kvantový stav, do kterého částice 3 přejde při měření Bellových stavů systému částic 1 a 2. Při tomto měření se totiž realizuje kvantový stav částice 2 a v důsledku entanglementu se musí změnit také kvantový stav částice 3. Právě díky tomuto provázání částic 2 a 3 se přenáší informace o původním kvantovém stavu částice 1. Entanglement částic 2 a 3 lze považovat za kvantový kanál přenosu informace.

V rovnici (22) vidíme, že pro \({\left| {{\psi ^ - }} \right\rangle _{12}}\) je opravdu \({\left| \psi \right\rangle _3}\) totožné s \({\left| \psi \right\rangle _1}\) až na znaménko (z kvantové mechaniky víme, že \({\left| \psi \right\rangle _3}\) a \(-{\left| \psi \right\rangle _3}\) reprezentují tentýž fyzikální stav). V ostatních případech (v dalších členech (22)) je pro měření Bellových stavů ještě potřeba unitární transformaceUnitární transformace – změna stavu kvantového systému, která odpovídá rotaci nebo zrcadlení v Hilbertově prostoru. , která výraz v kulaté závorce převede do tvaru \({\left| \psi \right\rangle _3}\) v rovnici (20). Formálně to představuje změnu znaménka, nebo vzájemnou výměnu \({\left| H \right\rangle _3}\) a \({\left| V \right\rangle _3}\), což se experimentálně realizuje vhodnými kombinacemi čtvrtvlnových a půlvlnových destiček.

Alice tak může, dle výsledků Bellova měření, jednoznačně Bobovi klasickým kanálem sdělit, kterou ze zmíněných unitárních transformací má na částici 3 provést, aby tak obdržel částici v kvantovém stavu, identickém s původním kvantovým stavem částice 1. Všimněme si, že Alice, ani nikdo jiný, předem vůbec nemuseli znát kvantový stav částice 1. Stejně tak byla irelevantní znalost polohy Alice a Boba. Podstatným je pouze sdílení EPR páru částic 2 a 3 (kvantový kanál) a možnost předání zprávy klasickým kanálem (například rádiem).

Kvantová teleportace z pohledu kvantové teorie informace

Zavedení qubitů vede nejenom k novému pohledu na čistě kvantový jev entanglementu, ale umožňuje nový způsob popisu procesů kvantové komunikace. Rolf Landauer si v roce 1998 jako první uvědomil, že kvantová informace má fyzikální podstatu. To samo o sobě představuje kvalitativně nový pohled na teorii informace jako takovou. Podle Landauera lze v důsledku výše zmíněného faktu považovat informatiku, či obecněji počítačovou vědu, ale dokonce i čistou matematiku za pouhá odvětví fyziky.

Rolf William Landauer (1927–1999)

Při kvantové teleportaci se obvykle přenáší jeden qubit (\(q\)) prostřednictvím dvou klasických bitů (2\(c\)), přičemž maximální entanglement qubitů (například EPR párů) se označuje jako ebit (\(e\)). V analogii s částicovou fyzikou lze na qubit nahlížet jako na virtuální částici \(q\). V analogii k antičásticím pak lze zavést rovněž antiqubit (\(\bar q\)). Na \(\bar q\) lze pohlížet jako na virtuální částici nesoucí zápornou informaci. Úplně analogicky můžeme považovat maximálně entanglovaný EPR pár za virtuálně konjugované částice e (ebit) a \(\bar e\) (antiebit). Příprava EPR páru se pak dá popsat jako vznik \(e\bar e\) páru z entropického vakua, tj. \(S\left( {e\bar e} \right) = 0\).

Členy EPR páru pak můžeme charakterizovat virtuálním informačním obrazem ±1 bit. Zde je důležité si uvědomit, že virtuální informační obsah ebitu může být konvertován do celé informace v interakci s qubitem a klasickými bity (cbity). Vzhledem k unitárnosti procesu kvantové teleportace nyní můžeme hovořit o konzervativním informačním toku. Takový popis je možný díky existenci záporných podmíněných entropií, jak ukážeme dále.

V analogii s částicovou fyzikou a kvantovou teorií pole lze jít dokonce ještě dál. Konkrétní kvantový informační proces se dá popsat jako interakce fyzikálních částic (qubitů a ebitů) při použití analogií Feynmanových diagramů.

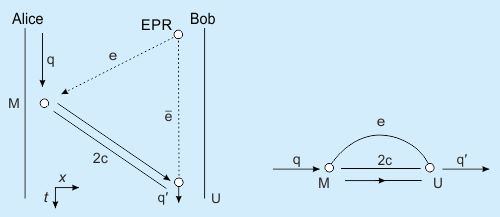
Obr. 1: Schéma kvantově informačního diagramu: Nalevo: Alice a Bob mají k dis­pozici entanglovaný \(e\bar e\) pár. Alice provede měření M neznámého (tele­por­to­va­ného) qubitu q a ebitu e ve dvoučásticové Bellově bázi, přičemž získá dva klasické bity (2c). Bob prostřednictvím dvou klasických bitů (2c) rozhodne, kterou ze čtyř unitátních transformací U na prostoru H (viz vztah (23)) použije v aplikaci na antiebit \(\bar e\) při rekonstrukci teleportovaného qubitu q′. Napravo: Popis téhož procesu pomocí Feynmanova diagramu. Zdroj: [1].

Ukažme si tedy, jak bude vypadat popis kvantové teleportace pomocí výše nastíněného formalizmu: při kvantové teleportaci je neznámá částice \(q\) transportována prostřednictvím přenosu dvou částic \(c\), přičemž Alice a Bob předem obdrželi pár \(e\bar e\). Alice provede měření (M) na neznámých částicích \(q\) a \(e\), které vlastní, ve dvoučásticové Bellově bázi. Výsledkem jsou dvě částice \(c\), které odešle Bobovi klasickým kanálem. Ten pak na základě těchto dvou cbitů aplikuje jednu ze čtyř unitárních transformací (U) na částici \(\bar e\), jíž vlastní:

\[\begin{array}{l} {U_0} = - \alpha {w_1} - \beta {w_2}\,;\\ {U_1} = - \alpha {w_1} + \beta {w_2}\,;\\ {U_2} = - \beta {w_1} + \alpha {w_2}\,;\\ {U_3} = \beta {w_1} + \alpha {w_2}\,, \end{array}\]

(23)

kde \(\alpha,\beta \in C, {\left| \alpha \right|^2} + {\left| \beta \right|^2} = 1,\) a \({w_i}, i = 1,2\), je báze v \(H\). Předpokládejme nyní, že informační tok zachovává entropii. Podle obr. 1 bude činnost Alice vyjádřena v (M) rovnicí

\[S\left( {2c} \right) = S\left( {qe} \right) = S\left( q \right) + S\left( e \right) = 1 + 1 = 2\,,\]

(24)

neboť \(q\) a \(e\) jsou nezávislé. Protože ale podmíněná entropie zbývající částice \(\bar e\) má hodnotu

\[S\left( {\bar e\left| {qe} \right.} \right) = - 1,\]

(25)

na straně Boba bude platit

\[S\left( {q'} \right) = S\left( {qe\bar e} \right) = S\left( {qe} \right) + S\left( {\bar e\left| {qe} \right.} \right) = 2 - 1 = 1\,,\]

(26)

kde \(q\)´ jsme označili qubit získaný Bobem, jenž je však samozřejmě informačně totožný s qubitem \(q\). V jazyce kvantové teorie pole můžeme částici \(\bar e\) nahradit částicí \(e\) pohybující se inverzně v čase (viz obr. 1). Pak je celý proces formálně ekvivalentní přenosu jednoho qubitu prostřednictvím dvou cbitů, avšak s využitím jednoho ebitu. Operace v M a U pak odpovídají vrcholům Feynmanova diagramu, popisujícím duální informaci zachovávající procesy

\[U:\quad 2c + \bar e \to q\,,\]	(27)
\[M:\quad q + e \to 2c\]	(28)

zcela ekvivalentní entropickým procesům (24) a (26). Stojí za povšimnutí, že tyto vztahy se nemohou objevit na vnějších částech diagramu, protože entanglovaný pár \(e\bar e\) neobsahuje čitelnou (měřitelnou) informaci, obdobně jako je tomu u virtuálních částic v kvantové teorii pole.

Kvantovou teleportaci se podařilo poprvé prakticky uskutečnit v roce 1997 v Innsbrucku, vědeckému týmu pod vedením Antona Zeilingera. Jednalo se o teleportaci polarizačního stavu jediného fotonu.

Anton Zeilinger (*1945)

V následujících letech byly úspěšně teleportovány i další částice a od roku 2004 dokážeme kvantově teleportovat celé atomy. V roce 2012 se čínským vědcům podařilo teleportovat shluk asi 100 milionů atomů rubidia o objemu cca. 1 mm³ na vzdálenost 150 metrů.

Nutno podotknout, že v posledním případě byla použita nová metoda teleportace, navržená v roce 2007. Ta nevyžaduje kvantové provázání, ale využívá Boseho-Einsteinův kondenzát (BECBEC – Boseho-Einsteinův kondenzát (Bose Einstein Condensate, BEC), představuje stav hmoty, ve kterém jsou všechny částice v jednom jediném kvantovém stavu. Vlnové funkce se vzájemně překrývají a při fázovém přechodu vznikne společná vlnová funkce. Soustava částic se začne chovat jako jediná „superčástice“. Boseova-Einsteinova kondenzace vzniká u bosonů, které se mohou nacházet všechny v nejnižším energetickém stavu. Na rozdíl od běžné kondenzace, jako je tomu u fázových přechodů plynů na pevné látky, jde o kondenzaci v prostoru hybností. Přechod od klasického stavu ke kvantovému je náhlý, až dramatický. Kvantové chování se projevuje při teplotě nižší, než je tzv. teplota degenerace.), ve kterém jsou částice na nejnižší energetické hladině a mají stejný kvantový stav. Na BEC se pustí teleportovaná hmota, jejíž částice také dosáhnou nejnižší energetické hladiny a nadbytečnou energii vyzáří jako světelný paprsek, obsahující veškerou informaci o teleportovaných částicích. Tento paprsek pak při kontaktu s jiným BEC vytvoří původní teleportovaný stav.

Jak funguje kvantový počítač. Video na kanálu Josh's na YouTube (20 minut).

K zásadnímu průlomu ve vývoji kvantového internetu došlo na počátku roku 2022, kdy konsorcium několika předních výzkumných institucí oznámilo první demonstraci trvalé, a vysoce věrné kvantové teleportace na dlouhé vzdálenosti. Fermilab, AT&T, Harvardská univerzita, NASA Jet Propulsion Laboratory, University of Calgary a Caltech, ohlásili úspěšnou teleportaci qubitů skrz 22 kilometrů optických vláken natažených mezi Caltech Quantum Network a Fermilab Quantum Network.



*  *  *

Všechny bulletiny této série

Odkazy