Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 37 – vyšlo 13. listopadu, ročník 15 (2017) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

37/2017

Kvantové počítače – principy

Petr Kulhánek

U počítačů založených na elektronických prvcích došlo v posledním půlstoletí k neuvěřitelnému rozmachu. Počítače se staly základním rysem soudobé civilizace. Razantní miniaturizace počítačových součástek probíhala mnoho desítek let podle tzv. Moorova zákonaMoorův zákon – pozorování Gordona Moora, jednoho ze spoluzakladatelů společnosti Intel, které říká, že počet tranzistorů na jednom čipu se přibližně každých 18 měsíců zdvojnásobí. Toto pozorování publikoval v roce 1965 s periodicitou 12 měsíců, v roce 1975 zákon upravil na dobu 18 měsíců. Nejedná se o přesný fyzikální zákon, ale toto tvrzení s malými odchylkami platilo až přibližně do roku 2015., a to až do okamžiku, kdy se velikost jednotlivých prvků stala souměřitelná s objekty mikrosvětaMikrosvět – svět malých rozměrů neuchopitelný lidskými smysly. V tomto světě platí zákony kvantové teorie, charakteristické jsou diskrétní hladiny některých veličin, dualismus vln a částic, nelokálnost objektů, superpozice jejich stavů a nekomutativnost příslušných teorií. a do jejich chování začaly zasahovat kvantové zákony. Další miniaturizace probíhá pomaleji než dříve a brzy prolomí hranici kvantového světa. Tento fakt neznamená konec rozvoje výpočetní techniky. Naopak, v mezičase se lidstvo naučilo manipulovat s jednotlivými atomy (viz např. AB 38/2012) a kvantové chování základních prvků integrovaných obvodů lze využít ke konstrukci počítačů zcela nového typu a zcela netušených možností. Ano, řeč je o kvantových počítačíchKvantový počítač – počítač využívající k zápisu informace kvantově mechanické vlastnosti částic, například spin elektronů, spin atomových jader nebo jiné vlastnosti kvantově se chovajících objektů. Kvantový počítač nese současně informaci o všech možných hodnotách kvantované veličiny, a tím provádí paralelně výpočet všech možností, které mohou nastat. Výpočet je mnohonásobně efektivnější než u klasického počítače. Základní jednotka informace se nazývá qubit (kvantový bit). Zatím jsou kvantové počítače ve stádiu ověřování principů., na jejichž vývoji v současnosti usilovně pracují v mnoha špičkových laboratořích po celém světě. První úspěchy zaplavují odborný tisk a ve vzduchu je cítit přicházející počítačová revoluce. Proto se v dnešním bulletinu pokusíme popsat základní principy těchto strojů blízké budoucnosti, v nichž křemíkové obvody nahradí kvantové částice.

Umělecká vize kvantového počítače, který manipuluje s jednotlivými atomy.
Zdroj: Cointelegraph.

Kvantový počítač – počítač využívající k zápisu informace kvantově mechanické vlastnosti částic, například spin elektronů, spin atomových jader nebo jiné vlastnosti kvantově se chovajících objektů. Kvantový počítač nese současně informaci o všech možných hodnotách kvantované veličiny, a tím provádí paralelně výpočet všech možností, které mohou nastat. Výpočet je mnohonásobně efektivnější než u klasického počítače. Základní jednotka informace se nazývá qubit (kvantový bit). Zatím jsou kvantové počítače ve stádiu ověřování principů. Kvantový bit, qubit – kvantová verze bitu (jednotky informace). Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Moorův zákon – pozorování Gordona Moora, jednoho ze spoluzakladatelů společnosti Intel, které říká, že počet tranzistorů na jednom čipu se přibližně každých 18 měsíců zdvojnásobí. Toto pozorování publikoval v roce 1965 s periodicitou 12 měsíců, v roce 1975 zákon upravil na dobu 18 měsíců. Nejedná se o přesný fyzikální zákon, ale toto tvrzení s malými odchylkami platilo až přibližně do roku 2015.

Vlastnosti mikrosvěta a kvantová logika

Objekty malých rozměrů mají pro nás některé nepředstavitelné vlastnosti. Především jde o objekty nelokální. V žádném případě si nemůžeme myslet, že jde o kuličky, které postupně procházejí jednotlivými body klasické trajektorie. Například elektron nemá v atomárním obalu konkrétní polohu, ve které by v daném okamžiku byl. Jeho nelokálnost (nejen v atomu) mu umožňuje dělat pro nás nepředstavitelné kousky. Může být na více místech naráz, dokáže projít současně dvěma otvory a z místa A se dostane do místa B, aniž by prošel mezilehlými body (takovému jevu někdy říkáme tunelování). Některé vlastnosti elektronu nemají vůbec žádný protějšek v makrosvětě. Typickým příkladem je spinSpin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole.. Každá makroskopická částice může mít nenulový moment hybnosti, který popisuje její oběh kolem určitého místa. Je-li částice nabitá, generuje tento otáčivý pohyb magnetické pole. V mikrosvětě má každá částice další podobnou vlastnost, které říkáme spin, a která se skládá s běžným momentem hybnosti. Tuto vlastnost si neumíme nijak představit, víme, že existuje a že je schopná u částic opět generovat magnetické pole, a to dokonce i tehdy, když nejsou nabité (příkladem může být neutron). Spin elektronu je orientován dvěma směry, takže při měření dostaneme jednu, nebo druhou hodnotu (magnetický moment odpovídající spinu elektronu míří jedním, nebo druhým směrem). Odpovídající stavy můžeme označit například nahoru | ↑ ⟩ a dolů. | ↓ ⟩. Ve skutečnosti jde o projekce spinu, neboť při jeho měření vždy měříme projekci do určitého směru. Nejprve se začala bouřlivě rozvíjet elektronika, která v zařízeních využívá náboje elektronu, později začal razantní nástup spintronikySpintronika – spinová elektronika neboli magnetoelektronika. Jde o technologii využívající kvantové vlastnosti spinu elektronu, případně celého atomu. Zatímco klasická elektronika využívá ve všech technologiích pouze náboj elektronu, ve spintronice se kromě náboje elektronu využívá i orientace jeho spinu. První spintronické logické obvody byly zkonstruovány v roce 1997., která dokáže v našich technologiích využívat i spin elektronu nebo celého atomu. Kvantové počítače patří právě k takovým technologiím. Spin umíme měřit díky jím generovaným magnetickým účinkům. Nejjednodušší měření je založeno na průletu částice nehomogenním magnetickým polem. Částice se spinem | ^ ⟩ se vychýlí na jednu stranu, zatímco částice se spinem | ˇ ⟩ se vychýlí na opačnou stranu. Částice s různou projekcí spinu, které prolétly magnetickým polem, proto dopadají do různých míst (detektorů). Takový experiment poprvé uskutečnili němečtí fyzici Otto Stern a Walter Gerlach v roce 1925. Dnes je možné vytříbenými postupy nejen měřit spin částic, ale dokonce s ním i manipulovat.

Senzor měřící spin částic ve vzorku. Spin elektronu v hrotu reaguje se spinem atomů v měřeném vzorku, což se projeví změnami ve světelném signálu. Z těchto změn se poté rekonstruuje spinová struktura vzorku. Zdroj: Basilejská univerzita.

Kvantová superpozice

Každý kvantový počítač využívá tři základní jevy z kvantového světa: superpozici, provázanost a interferenci. Princip superpozice je v mikrosvětě důsledné uplatňován. Objekty mikrosvěta mohou být ve více stavech naráz a teprve v okamžiku měření se realizuje jeden z možných stavů, který je výsledkem tohoto měření. V našem příkladu s elektronem, který má dvě projekce spinu, dojde k tomu, že se šíří v superpozici

α | ^ ⟩ + β | ˇ ⟩.

Koeficienty α, β určují, jak „moc“ je který stav v kombinaci zastoupený. V klasické fyzice by šlo o čísla z intervalu <0, 1>, pro která platí α + β = 1 a která bychom interpretovali jako pravděpodobnosti výsledku měření. Například α = 1, β = 0 by znamenalo, že s jistotou naměříme stav se spinem „nahoru“. Kvantová teorie takto jednoduše ale nefunguje. Koeficienty superpozice jsou obecně komplexní čísla a mají význam amplitud pravděpodobností. Skutečné pravděpodobnosti jsou druhou mocninou amplitudy těchto komplexních čísel (viz obrázek), tedy |α|² a |β|². Součet všech pravděpodobností musí být rovný jedné, proto v kvantové teorii platí |α|² + |β|² = 1. Uvažujme jako příklad kvantovou superpozici s koeficienty α = 1/√2, β = 1/?2. Při měření mají obě možnosti stejnou pravděpodobnost, která je rovna 1/2. Pokud by koeficienty superpozice byly α = 1/2, β = ?3/2, budou příslušné pravděpodobnosti 1/4 a 3/4. Jak už jsme si uvedli, koeficienty superpozice nemusí být reálná čísla, může jít o komplexní čísla, z nichž každé je reprezentováno amplitudou a fází. Pravděpodobnosti jsou samozřejmě reálné nezáporné (jsou dány druhou mocninou amplitudy komplexního čísla).

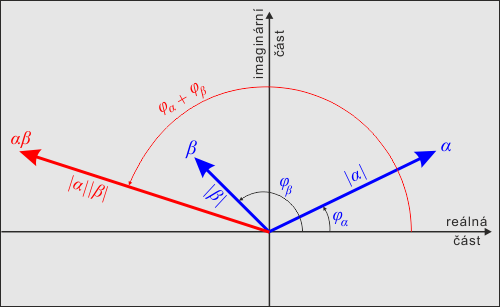
Každé komplexní číslo lze reprezentovat amplitudou (velikostí, vzdáleností od počátku) a fází (úhlem mezi vodorovným směrem a spojnicí počátku s komplexním číslem). Amplitudu komplexního čísla označujeme symbolem absolutní hodnoty. Součin dvou komplexních čísel má amplitudu rovnou součinu obou amplitud a fázi rovnou součtu obou fází.

Kvantová provázanost

V bulletinu AB 33/2017 věnovanému teleportaci jsme se zmínili o provázanosti objektů, při níž mají dva objekty společnou vlnovou funkci. Například dva elektrony, které mají společný původ, mohou mít provázané kvantové stavy. Provázané kvantové stavy je možné uměle navodit také za pomoci mikrovlnného nebo laserového impulzu. Výsledkem provázanosti je společný stav obou elektronů, který je superpozicí čtyř možností:

α | ^^ ⟩ + β | ^ˇ ⟩ + γ | ˇ^ ⟩ + δ | ˇˇ ⟩.

V zápise odpovídá první šipka prvnímu elektronu a druhá druhému. Pokud jsou například koeficienty α, δ nulové, budou mít spiny vždy opačnou hodnotu. Provedeme-li u takto připraveného systému měření na jednom z elektronů, automaticky budeme vědět, že druhý je v opačném spinovém stavu. Právě tento fakt se využívá u teleportace (viz AB 33/2017) i u kvantových počítačů. V klasickém počítači je informace uložena do nul a jedniček. Ty mohou být reprezentovány například určitým napětím na elektrodě nebo orientací magnetické domény v magneticky aktivním materiálu harddisku či jiného média. S těmito nulami a jedničkami poté děláme základní operace (například logickou negaci (NOT), logický součin (AND) nebo logický součet (OR). Pro určitou kombinaci nul a jedniček na vstupu je dána konkrétní kombinace nul a jedniček na výstupu (viz ukázka v následující tabulce). U kvantového počítače je informace nesena v celé superpozici stavů, tzv qubitemQubit – kvantová verze bitu neboli kvantový bit, základní jednotka informace podléhající kvantové logice. Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Element kvantové informace zavedl Benjamin Schumacher roku 1995. Na qubit lze také pohlížet jako na virtuální částici a v analogii k antičásticím lze zavést rovněž antiqubit nesoucí zápornou informaci.. Paralelně je nesena informace o všech koeficientech superpozice. V případě provázanosti dvou qubitů máme k dispozici 4 koeficienty (viz poslední vztah). Podaří-li se nám provázat N qubitů, je počet koeficientů 2^N, tj. pro 50 provázaných qubitů je počet koeficientů 2⁵⁰ ≈ 10¹⁵, tedy více informací, než je schopen pojmout jakýkoli klasický počítač. Samozřejmě, že příprava velkého množství provázaných qubitů a jejich udržení po dostatečně dlouhou dobu je velkým technickým problémem. Logické operace s qubity se zpravidla uskutečňují působením laserového nebo mikrovlnného impulzu či magnetickým polem. Při takových operacích se mění amplituda a fáze koeficientů superpozice. Operace je přirozeným způsobem paralelní (probíhá se všemi koeficienty superpozice), což umožňuje vytvářet účinné algoritmy řešení problémů. Zejména typické nepolynomiální úlohy, například faktorizace čísla (jeho rozklad na prvočinitele) by měla z exponenciální složitosti přejít u kvantového počítače na polynomiální složitost. Prolomení různých šifrovaných kódů by pro kvantový počítač mohlo být hračkou. Čtyři příklady logických operací s jedním jediným qubitem na vstupu a jedním na výstupu jsou v druhé části následující tabulky:

operace s bity	vstup 1	vstup 2	výstup
NOT	0	–	1
	1	–	0
AND	0	0	0
	0	1	0
	1	0	0
	1	1	1

Ukázka klasických operací NOT (jeden vstup a jeden výstup) a AND (dva vstupy,
jeden výstup). Operace jsou realizovány elektronickými obvody, tzv. hradly.

operace s qubitem	vstup	výstup
Pauliho X hradlo (NOT)	(α, β)	(β, α)
Pauliho Y hradlo	(α, β)	(i β, −i α)
Pauliho Z hradlo (flip)	(α, β)	(α, -β)
Hadamard	(α, β)	(α + β, α -β)/?2

Ukázka kvantových operací s jedním qubitem. V kulatých závorkách jsou koeficienty superpozice – v prostředním sloupci před operací a v posledním sloupci po operaci. Operace s qubity se zpravidla realizují za pomocí laserového nebo mikrovlnného impulzu. Také je možné využít magnetické pole.

Kvantová interference

Systém, který je v superpozici stavů, se až do měření může vyvíjet mnoha způsoby. Amplitudy pravděpodobnosti jednotlivých možností se sčítají, pravděpodobnost konkrétní superpozice je dána druhou mocninou velikosti výsledné amplitudy pravděpodobnosti. Jednotlivé stavy superpozice spolu interferují, což znamená, že probíhá jak destruktivní interference (pravděpodobnosti některých možností se snižují), tak konstruktivní interference (pravděpodobnosti některých možností se zvyšují). Situace je podobná, jako když se světlo šíří z bodu A do bodu B. Podle kvantové teorie se může šířit po libovolné trajektorii, tj. paralelně prochází mnoha trajektoriemi. Většina z nich má ale díky destruktivní interferenci s okolními trajektoriemi zcela mizivou pravděpodobnost. Ta trajektorie, kterou okolní trajektorie konstruktivní interferencí zesílí, bude realizována v přírodě. Je to trajektorie, kterou světlo urazí za nejkratší čas (tzv. Fermatův princip) – u ní jsou fáze blízkých trajektorií blízké a dochází ke konstruktivní interferenci. K obdobné interferenci dochází při kvantovém výpočtu. Některá z možností se natolik zesílí konstruktivní interferencí, že ji při finálním měření na systému qubitů nalezneme jako výsledek námi zadané úlohy.

Současný stav

Od prvních úvah z 80. let 20. století uplynulo velké množství času. První experimenty se konaly s ultrachladnými ionty zachycenými v důmyslných pastech z elektrických a magnetických polí. Tyto ionty představovaly jednotlivé qubity. Vědci ale zkoušeli i qubity založené na samotných elektronech nebo dokonce elektronových děrách. V letošním roce se společnostem IBM a INTEL podařilo nezávisle vyvinout prototyp procesoru s 17 provázanými qubity. Budoucí kvantový počítač společnosti IBM je vyvíjen pod názvem IBM Q. Jinou cestou se vydali kanadští odborníci z INRS (National Institute of Scientific Research), kteří letos vytvořili dva provázané qubity, každý z nich byl ale v superpozici deseti stavů, což odpovídá storozměrnému poli čísel. Vzniklo také několik simulátorů kvantových výpočtů, s nimiž lze na klasických počítačích simulovat kvantový výpočet (výpočet neprobíhá paralelně, ale jen sekvenčně a samozřejmě velmi pomalu). Jeden z nich vyvinuli na Harvardu, jiný implementovala do svého Visual Studia společnost Microsoft. O experimentálním úsilí o konstrukci kvantového počítače si povíme někdy příště. Kvantové počítače klepou na dveře a jejich nástup lze očekávat již v blízké budoucnosti.

Kanadský mikročip, který dokáže připravit dva provázané qubity,
z nichž každý má 10 stavů. Zdroj: INRS, 2017.

Principy kvantového počítání. Zdroj: IBM, 2017 (mp4, 17 MB)

Odkazy