|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Teleportace
Petr Kulhánek
Už se vám stalo, že jste někdy někde byli, a přitom jste potřebovali být úplně někde jinde? V takovém případě by se šikl hodně rychlý transport na kýžené místo. Pokud možno nadsvětelnou rychlostí a ještě lépe nekonečnou rychlostí, tedy okamžitě. Zmizet na jednom místě a objevit se na jiném. Tuto touhu zpodobňuje mnoho vědeckofantastických povídek a románů. Autoři hovoří o teleportaci. Člověk se zavře do teleportačního zařízení a z něho vystoupí na druhém konci vesmíru. Posledních deset let se dosti často v médiích hovoří o tom, že vědci teleportovali foton, elektron či dokonce celý atom. Nejprve to byly desítky centimetrů, poté kilometry a nyní už stovky a tisíce kilometrů. Jsme snad svědky splněného snu mnoha generací? Bohužel nikoli. Ve skutečnosti nejde o přenos hmoty, ale o přenos kvantové informace, a to je velký rozdíl. Přenáší se informace v podobě qubitůQubit – kvantová verze bitu neboli kvantový bit, základní jednotka informace podléhající kvantové logice. Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Element kvantové informace zavedl Benjamin Schumacher roku 1995. Na qubit lze také pohlížet jako na virtuální částici a v analogii k antičásticím lze zavést rovněž antiqubit nesoucí zápornou informaci. a podle této informace se na jiném místě pořídí více či méně zdařilá kopie originálu. Při této proceduře ale originál při měření jeho stavu zanikne. Kvantovou informaci nelze jen tak přenést (zkopírovat) jinam. K pořízení zmíněné kopie navíc potřebujete klasický kanál, tedy alespoň část informace musí být na druhé místo odeslána klasickým způsobem, maximálně rychlostí světla. V žádném případě kvantová teleportace není teleportací věcí, jak ji známe ze scifi literatury a už vůbec neprobíhá nekonečnou rychlostí. Konkrétně u atomů se dokonce kopírují jen vlastnosti obalu (pořízená kopie bude mít stejná kvantová čísla) a vůbec se nehledí na stavy jader zaniklého originálu a vytvořené kopie. Vzdáleně to připomíná poslání fotografie hrocha, kterého si podle ní uplácáme ze sádry na jiném místě. Hroch jako hroch. A že není živý? Nevadí. V každém případě jde o mimořádně užitečnou technologii, o které nepochybně uslyšíme stále častěji.

Umělecká vize kvantové teleportace, v tomto případě jde o teleportaci kočky. Ale je
to jedno, hrošice či jalová kráva by posloužily stejně dobře. Zdroj: Live
Science.
|
Kvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí respektovat omezení kvantové mechaniky na současnou měřitelnost či neměřitelnost veličin. Například základní energetický stav atomu značíme symbolem |S>, vakuový stav symbolem |0>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně. Kvantový stav je zpravidla charakterizován sadou kvantových čísel a je matematicky vyjádřen tzv. vlnovou funkcí (prvkem Hilbertova prostoru stavů). Superpozice stavů – pokud dva stavy představují fyzikálně realizovatelný stav systému, je možná i superpozice těchto stavů. Například kvantově mechanická kočka nemusí být jen živá nebo mrtvá, může být i „obojí zároveň“. Takový stav značíme a|Ž⟩+b|M⟩, kde a a b jsou čísla vyjadřující váhu. Pokud na kočce v tomto superponovaném stavu provedeme měření, s pravděpodobností |a|2 ji najdeme živou a s pravděpodobností |b|2 mrtvou. Kvantová superpozice stavů je běžná pro kvantové objekty, například elementární částice nebo atomy. U makroskopických objektů (kočka, člověk) komunikujících s okolím je nemožná. Kvantová interference – skládání amplitud pravděpodobnosti několika možností vývoje systému. Amplitudy se mohou vyrušit, potom hovoříme o destruktivní interferenci. Pravděpodobnosti dějů jsou druhou mocninou součtu amplitud pravděpodobností jednotlivých možností. Kvantový bit, qubit – kvantová verze bitu (jednotky informace). Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Kolaps vlnové funkce – je-li kvantový systém v superponovaném stavu, nemůžeme jeho stav přímo zjistit. Při měření v určité bázi si systém náhodně vybere některý z bázových stavů a skokem do něj přejde. Říkáme, že jeho vlnová funkce zkolabovala. Například měření na stavu |0>+|1> způsobí s 50 % pravděpodobností přechod systému do stavu |0> a se stejnou pravděpodobností do stavu |1>. |
Nelokálnost mikrosvěta
To, že v mikrosvětě platí pro člověka nezvyklé zákony, je všeobecně známé. Objekty mikrosvěta nelze připodobnit ani k pomeranči, ani k výše zmíněné hrošici, která genderově vyrovnává hrocha použitého ještě výše. Jedna jejich vlastnost je nám ale obzvláště nepříjemná (lépe řečeno těžko představitelná). Objekty mikrosvěta jsou totiž nelokální. Neutron může projít dvěma štěrbinami současně, foton může být současně ve dvou ramenech interferometru, elektron je ve všech místech elektronového obalu naráz, a svisle vržený atom se může nacházet ve dvou výškách. Kéž bychom to uměli i my lidé: být současně v hospodě i na pracovišti, střízliví i opilí, to by zmátlo leckterého úředníka a jeho hodnotící tabulky by se také rázem ocitly v superpozici stavů a byly by k ničemu. Právě nelokálnost je klíčem k mnoha jevům, které se nám na první pohled zdají nemožné. Měřením vlastností objektu v jednom místě se dozvídáme informace o jeho chování v místě jiném. A navíc má vše pravděpodobnostní charakter a my se dozvíme, v jakém je objekt stavu až skutečným měřením. Lépe řečeno, v okamžiku měření ho do tohoto stavu přivedeme. Právě na tom je založena tzv. kodaňská interpretace kvantové teorie. Objekt je v superpozici mnoha nelokálních stavů a teprve aktem měření získá některý z těchto stavů. Pokud objekt popisujeme vlnovou funkcí, hovoříme o tom, že při měření dojde ke kolapsu vlnové funkceKolaps vlnové funkce – je-li kvantový systém v superponovaném stavu, nemůžeme jeho stav přímo zjistit. Při měření v určité bázi si systém náhodně vybere některý z bázových stavů a skokem do něj přejde. Říkáme, že jeho vlnová funkce zkolabovala. Například měření na stavu |0>+|1> způsobí s 50 % pravděpodobností přechod systému do stavu |0> a se stejnou pravděpodobností do stavu |1>. do jednoho z mnoha stavů předchozí superpozice. V kvantové teorii je poprvé akt měření, a tím i pozorovatel, součástí teorie samotné a měření ovlivňuje chování objektu.
Pokud rozdělíme světlo laseru a k cíli se bude dostávat po dvou různých drahách, může se stát, že v některém místě dojde k destruktivní interferenci a signál detektoru zcela vymizí a v jiném místě dojde ke konstruktivní interferenci a signál bude maximální, tedy do tohoto místa budou dopadat fotony. Opět jde o ukázku nelokálnosti – fotony se nacházejí současně v obou možných trajektoriích neboli v superpozici obou možných stavů (jedna a druhá dráha). V detektoru, kde se obě možné dráhy setkávají, poté interferujíKvantová interference – skládání amplitud pravděpodobnosti několika možností vývoje systému. Amplitudy se mohou vyrušit, potom hovoříme o destruktivní interferenci. Pravděpodobnosti dějů jsou druhou mocninou součtu amplitud pravděpodobností jednotlivých možností. samy se sebou, a v některých místech proto signál je, a v jiných není. Přitom nejde po porušení zákona zachování energie. Ta prostě není všude, energie elektromagnetického pole se vynoří jen v některých místech prostoru (detektorech).

Dvojštěrbinový experiment. Objekty mikrosvěta procházejí naráz oběma
štěrbinami
Výsledkem je interferenční obrazec na stnítku. Kresba: Ivan
Havlíček.
Skryté parametry
Část fyziků kritizovala nelokálnost kvantové teorie a náhodnost výsledků. Tuto skupinu asi nejvíce reprezentoval Albert Einstein, který se s výše zmíněnými vlastnostmi kvantové teorie nesmířil a předpokládal, že kvantová teorie není úplná. Náhodnost výsledku při měření by mohla souviset s tím, že systém má nějaké další, tzv. skryté parametry, díky jejichž neznalosti dochází k zdánlivě náhodnému výsledku aktu měření. V roce 1964 irský fyzik John Stewart Bell (1928–1990) ukázal, že statistické vlastnosti měření polarizace fotonuPolarizace fotonu – rovina kmitů elektrického pole, fotony jako kvanta příčného elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný stav fotonu je potom lineární kombinací obou polarizačních stavů v dané bázi. budou v případě teorie se skrytými parametry jiné než při standardní kvantové interpretaci. Matematickým vyjádřením je tzv. Bellova nerovnost, kterou musí splňovat střední hodnoty opakovaných měření, pokud existují skryté parametry a výsledky měření jsou předem dány.
První experimenty, které vedly na porušení Bellových nerovností, byly uskutečněny už v roce 1972, nicméně fyzikální komunita je nepovažovala za průkazné. Přesvědčivý důkaz neplatnosti Bellových nerovností a tedy nemožnosti existence skrytých parametrů v kvantové teorii podala až skupina Alaina Aspecta ve francouzském Orsay v experimentech prováděných v letech 1976 až 1983. V těchto experimentech excitovali za pomoci laserových impulzů atomy vápníku. Excitovaný elektron se vracel na původní hladinu přes mezistav, při prvním přechodu vyzářil foton s vlnovou délkou 551,3 nm, při druhém foton s vlnovou délkou 422,7 nm. Jak excitovaný, tak původní stav měly celkový moment hybnosti nulový, zatímco mezistav měl celkový moment hybnosti nenulový, což vedlo k určité vazbě mezi polarizacemi obou vyslaných fotonů. Ukázalo se, že Bellovy nerovnosti neplatí a náhodné výsledky experimentů nejsou důsledkem skrytých parametrů, ale základní vlastností přírody samotné. Podrobněji se o Bellových nerovnostech dozvíte v učebnici [1] nebo ve vynikajících popularizačních textech [2–5].

Zakladatelé kvantové teorie na konferenci v Solvay (1927), kde byla bouřlivě diskutovánna interpretace rodící se kvantové teorie. První řada: I. Langmuir, M. Planck, M. Curie, H. Lorentz, A. Einstein, P. Lanagevin, C. Guye, C. Wilson, O. W. Richardson. Druhá řada: P. Debye, M. Knudsen, W. Bragg, H. Kramers, P. Dirac, A. Compton, L. Broglie, M. Born, N. Bohr. Třetí řada: A. Piccard, E. Henriot, P. Ehrenfest, E. Herzen, T. Donder, E. Schrödinger, E. Verschaffelt, W. Pauli, W. Heisenberg, R. H. Fowler, L. Brillouin.
Provázanost stavů a EPR paradox
Odpor části fyziků k rodící se kvantové teorii vyústil v roce 1935 k formulaci myšlenkového experimentu, který měl demonstrovat neúplnost kvantové teorie a ukázat, že kvantová teorie je vnitřně sporná a bude muset být nahrazena lepší teorií mikrosvěta. U zrodu tohoto myšlenkového experimentu stáli Albert Einstein (1879–1955), ruskoamerický fyzik Boris Podolsky (1896–1966) a americko-izraelský fyzik Nathan Rosen (1909–1995). Podle počátečních jmen autorů se hovoří o tzv. EPR paradoxu. Dnes se nejčastěji používá formulace Davida Bohma, která pochází z roku 1951. Představme si částici s celkovým momentem hybnosti 0, která se rozpadne na dvě od sebe letící částice A a B, z nichž každá má spin 1. Orbitální moment obou částic je nulový (letí od sebe), a proto zákon zachování celkového momentu hybnosti vede na podmínku, že pokud naměříme u jedné z částic projekci spinu do libovolné osy 1, musí mít druhá částice projekci do téže osy -1, a naopak. Zdánlivý paradox vznikne tím, že provedením měření projekce spinu na jedné částici se okamžitě dozvíme projekci spinu u druhé částice, ať je jakkoli daleko. Na první pohled to vypadá, jakoby se informace šířila okamžitě, což odporuje principu kauzality (příčinnosti) ze speciální relativity. Na vině je opět tolik diskutované nelokální chování částic. Při měření na jedné částici zkolabuje vlnová funkce v celém prostoru, a to se projeví při následujícím měření na druhé částici. Obě částice jsou v tzv. provázaném stavuProvázaný stav – entanglement, kvantově korelovaný stav systému dvou a více částic, v němž nemá smysl mluvit o stavech jednotlivých složek. Například z provázaného stavu dvojice fotonů nelze vyjádřit stavy jednotlivých fotonů. Značíme |AB>+|XY>, což znamená, že najdeme-li první částici ve stavu A, je druhá ve stavu B. Je-li první ve stavu X, pak druhá je ve stavu Y. Měřením provedeným na jedné částici se dozvíme určitou informaci o částici druhé. Je to způsobeno tím, že mají společnou minulost. Někdy se také hovoří o propletených stavech. – mají společnou nelokální vlnovou funkci.
EPR paradox se často formuluje za pomoci polarizace dvou fotonů. Polarizací fotonu nazýváme rovinu kmitů elektrického pole. Ta se obecně může stáčet, nebo být fixní – pak hovoříme o rovinné polarizaci. Fotony, jakožto kvanta příčného elektromagnetického vlnění, mohou mít dvě nezávislé, navzájem kolmé rovinné polarizace. Skutečný stav fotonu je potom lineární kombinací obou polarizačních stavů v dané bázi. Měření polarizace fotonu lze uskutečnit například pomocí hranolu z islandského vápence, který je dvojlomný, a světelný paprsek se v něm proto dělí na řádný a mimořádný. Fotony putující ve směrech řádného a mimořádného paprsku mají navzájem kolmou polarizaci. Jinými slovy: islandský vápenec může fungovat jako registrační přístroj. Uvažujme nyní zjednodušený experiment: předpokládejme, že atom má celkový moment hybnosti nulový a po jeho excitaci ho opustí dva fotony, jejichž polarizace je korelována, v našem případě budeme dokonce předpokládat, že fotony mají přesně opačnou polarizaci. Pokud na jednom fotonu naměříme v nějaké bázi „vodorovnou“ polarizaci (například ve směru osy x), bude polarizace druhého fotonu „svislá“ (ve směru osy y) a naopak. Je jasné, že jde o stejnou formulaci jako dříve, jen je projekce spinu nahrazena polarizací fotonu (ta ale nakonec stejně závisí na projekci spinu fotonu do směru jeho pohybu). Výsledek měření není dopředu dán, je zcela náhodný. Jakmile ale provedeme měření na jednom fotonu, stav zkolabuje do jedné z obou možností a měření na druhém fotonu dá už jen doplňkový výsledek, ať je tento foton fyzicky lokalizován kdekoli. Stejný výsledek dostaneme i při volbě jiné báze, tj. měření budeme provádět pomocí polarizátoru otočeného o libovolný úhel. Při jakémkoli natočení hranolu budeme mít padesátiprocentní pravděpodobnost, že naměříme foton A s „vodorovnou“ polarizací a foton B se „svislou“ polarizací, a padesátiprocentní pravděpodobnost, že měření dopadne opačně.
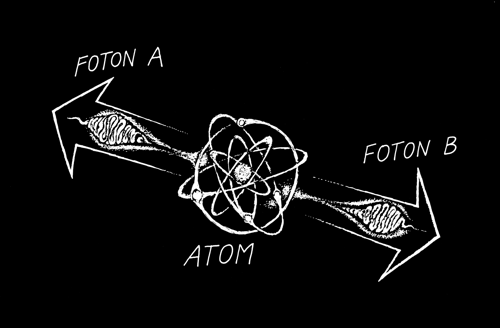
EPR paradox formulovaný za pomoci polarizace dvou fotonů. Kresba: Ivan Havlíček.
Kvantová teleportace
Pro kvantovou teleportaci se nabízí jednoduchá představa: na jednom místě zjistíme přesně stav určitého objektu a podle tohoto kvantového měření vybudujeme v jiném místě kopii. Tak jednoduché to ale není. Žádné kvantové měření nemůže být dokonalé. Nikdy například nemůžeme současně zjistit polohu a rychlost objektu, což je vlastnost mikrosvěta popsaná Heisenbergovými relacemi neurčitostiRelace neurčitosti – v mikrosvětě není možné současně změřit polohu a hybnost objektů. Změření jedné veličiny naruší měření druhé veličiny. Čím přesněji zjistíme polohu, tím menší informaci budeme mít o hybnosti a naopak. Jde o principiální zákonitost kvantového světa, která souvisí s nekomutativností veličin na elementární úrovni. Relace neurčitosti objevil Werner Heisenberg. Stejné relace platí také mezi energií a časovým intervalem. Ve vakuu mohou po velmi krátkou dobu vznikat ve shodě s relacemi neurčitosti fluktuace (objekty) o určité energii. Čím vyšší energie, tím kratší doba života těchto fluktuací. Dále relace platí i pro jakoukoli zobecněnou souřadnici a její hybnost. Může jít například o nějaké pole, které nemůže mít současně nulovou hodnotu a nulovou hybnost, což vede k jeho vakuovým fluktuacím.. Na kvantovou teleportaci se proto musí jít od lesa. Možný mechanizmus poprvé popsali v roce 1993 Charles Bennett, Gilles Brassard a další v článku [13], který měl pouhé 4 stránky, ale předznamenal zcela novou a revoluční technologii. Jako skenovací zařízení originálu totiž využili EPR pár provázaných částic. Vynecháme-li matematický popis procedury, lze ji zjednodušeně rozložit do čtyř kroků (detaily nalezne čtenář v literatuře):
- Vytvoříme EPR pár provázaných částic, jednu transportujeme do laboratoře A a druhou do laboratoře B. Tím jsme vytvořili „teleportační zařízení“. Bez něho není teleportace možná. Z toho je patrné, že teleportaci nelze uskutečnit do místa, které jsme nikdy předtím nekontaktovali.
- Teleportovaný objekt kvantově provážeme s tou částí EPR páru,
která se nachází v laboratoři A. Technicky je to možné pro elementární
částice, atomy a jednoduché molekuly. Následně provedeme měření stavu
provázané dvojice (objekt + jedna část EPR páru) v laboratoři A,
výsledkem je jeden z tzv.
Bellových stavůBellovy stavy – 4 propletené stavy dvojice qubitů.
Φ1 = |0112> + |1102>
Φ2 = |0112> − |1102>
Ψ1 = |0102> + |1112>
Ψ2 = |0102> − |1112>
Bellovy stavy tvoří bázi 4-rozměrného Hilbertova prostoru.. Při tomto měření se originál zničí. - Klasickým kanálem sdělíme výsledek měření do laboratoře B, kde teleportační inženýři vytvořili obdobný provázaný pár objektu (materiálu ke stavbě kopie) s druhou částí EPR páru. Tuto operaci nelze provést kvantovým kanálem, kvantová informace založená na pouhých amplitudách pravděpodobnosti je nepřenositelná.
- Podle výsledku měření v laboratoři A se dozvíme, v jakém ze čtyř možných Bellových stavů se nachází provázaná dvojice v laboratoři B. Pro každou z těchto možností existuje klíčová operace (například průchod vhodně nastaveným polarizátorem), která uvede objekt do stavu shodného se zaniklým teleportovaným originálem.
Celá procedura může být o něco jednodušší. Pokud jsou všechny částice stejné, může být druhá část EPR páru v laboratoři B rovnou použita jako stavební materiál pro kopii originálu. K teleportaci pak postačí pouze tři částice: kvantově provázané částice B a C tvořící EPR pár a originál A. Originál A provážeme s částicí B a provedeme měření jejich stavu v nějaké bázi. Výsledek měření přeneseme klasickou cestou do místa, kde se nachází částice C. Vhodnými operacemi uděláme z částice C kopii částice A (ta v průběhu procedury zanikla).

Princip Bennettovy-Brassardovy teleportace. Mezi oběma místy musí existovat
klasický informační kanál. Zdroj: Nature.
Experimentální realizace
První experimenty s kvantovou teleportací probíhaly na Innsbrucké univerzitě v roce 1997. Dirk Bouwmeester, Anton Zeilinger a další zde na laboratorním stole ukázali, že je možná teleportace ultrafialových fotonů a že mechanizmus navržený Bennettem a dalšími v roce 1993 je životaschopný. Slavný innsbrucký experiment odstartoval obrovské množství dalších pokusů s kvantovou teleportací. Teleportovány byly nejen fotony, ale i celé atomy nebo jejich shluky. Zaměřme se jen na nejvýznamnější experimenty tohoto druhu. V roce 2004 se podařilo odborníkům z Vídeňské univerzity teleportovat fotony na opačný břeh Dunaje na vzdálenost 600 metrů. Jako klasický kanál posloužil optický kabel, který spojil obě laboratoře. Není bez zajímavosti, že místy byl tažen městskou kanalizací. V roce 2010 se v Číně uskutečnila teleportace fotonů na vzdálenost 16 kilometrů a bylo jasné, že teleportace bude možná i na obrovské vzdálenosti. V roce 2012 se podařilo vědcům z Vídeňské univerzity vedeným Antonem Zeilingerem teleportovat fotony mezi Kanárskými ostrovy La Palma a Tenerife na vzdálenost 143 kilometrů. Vrcholem tohoto trendu se stala teleportace fotonů na oběžnou dráhu v červenci tohoto roku (2017). Čínští vědci úspěšně teleportovali fotony mezi pozemní stanicí a družicí MiciusMicius – čínská družice pro kvantové technologie, která byla na oběžnou dráhu vynesena dne 17. srpna 2016 na palubě nosné rakety Dlouhý pochod 2D. Oficiální název družice je QUESS (QUantum Science Experiment Satellite). V červenci 2017 se podařila kvantová teleportace fotonů na vzdálenost 1 400 kilometrů. Téhož roku se uskutečnila distribuce kvantového klíče šifrované zprávy na vzdálenost 7 500 kilometrů. Alternativní název Micius je vytvořen ze jména čínského filosofa ze 4. století před naším letopočtem., maximální vzdálenost při experimentech byla 1 400 kilometrů. Úspěšně bylo provedeno 900 teleportací.
V mezičase byly navrženy i jiné mechanizmy teleportace, například využívající namísto provázání stavů BECBEC – Boseho-Einsteinův kondenzát (Bose Einstein Condensate, BEC), představuje stav hmoty, ve kterém jsou všechny částice v jednom jediném kvantovém stavu. Vlnové funkce se vzájemně překrývají a při fázovém přechodu vznikne společná vlnová funkce. Soustava částic se začne chovat jako jediná „superčástice“. Boseova-Einsteinova kondenzace vzniká u bosonů, které se mohou nacházet všechny v nejnižším energetickém stavu. Na rozdíl od běžné kondenzace, jako je tomu u fázových přechodů plynů na pevné látky, jde o kondenzaci v prostoru hybností. Přechod od klasického stavu ke kvantovému je náhlý, až dramatický. Kvantové chování se projevuje při teplotě nižší, než je tzv. teplota degenerace. kondenzát, kde je možná teleportace stavu obrovského množství atomů. V roce 2004 byla otestována další varianta teleportace, šlo o pětici provázaných fotonů, což poprvé umožnilo rekonstrukci originálu ve více laboratořích. Na experimentu se podíleli vědci z Hefejské národní laboratoře (Čína), Innsbrucké univerzity (Rakousko) a Heidelberské univerzity (Německo). Kvantová teleportace je dnes šlágrem současné vědy a vůbec se není čemu divit. Vždyť zvládnutí přenosu kvantového stavu na velké vzdálenosti může znamenat pokrok nejen ve vývoji kvantových počítačů a v šifrování, ale také v technologiích pro celosvětovou informační síť internet, která by se mohla proměnit v médium zcela nedozírných možností.

Optická lavice s kvantovou teleportací v Centru pro kvantovou
fotoniku na Bristolské
univerzitě. Délka experimentu je 4,2 metru.
Fotografie pochází z roku 2013.

První kvantová družice, čínský Micius neboli QUESS.Cílem není
jen kvantová
teleportace, ale i kvantové šifrování a testování Bellových
nerovností. Zdroj: CN.
Odkazy
- Petr Kulhánek: Vybrané kapitoly z teoretické fyziky; Kvantová teorie; AGA 2016
- Pavel Cejnar, Miloslav Dušek: Kvantové hlavolamy; Vesmír 77, 1998
- Dana a Rudolf Mentzlovi: Jak funguje kvantová teleportace - I.část; idnes.cz, 14. 12. 2016
- Dana a Rudolf Mentzlovi: Jak funguje kvantová teleportace - II.část; idnes.cz, 21. 12. 2016
- Vojtěch Hála: Kvantová teleportace; AB 31/2004
- Jesse Emspak: Chinese Scientists Just Set the Record for the Farthest Quantum Teleportation; Live Science, 14 Jul 2017
- Ji-Gang Ren et al.: Ground-to-satellite quantum teleportation; arXiv:1707.00934 [quant-ph], 4 Jul 2017
- Xiao-Song Ma et al.: 143 km: Physicists break quantum teleportation distance; University of Viennna/PhysOrg; 5 Sep 2012
- The Quantum Teleportation Race Goes Into Space in 2016; SciTechDaily, 7 Dec 2012
- Carlos Mochon: Introduction to Quantum Teleportation; Light Like
- Avery Thompson: How Quantum Teleportation Actually Works; Popular Mechanics; 16 Mar 2017
- Wikipedia: Quantum Teleportation
- Charles H. Bennett, Gilles Brassard, Claude Crépeau, Richard Jozsa, Asher Peres, William K. Wootters: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels; Phys. Rev. Lett. 70, 1895, 29 Mar 1993
