|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Rydbergovy atomy simulují trojanské asteroidy
David Břeň
Kromě známých objektů, jako jsou planetyPlaneta – nebeské těleso, které: 1) obíhá okolo Slunce. 2) má dostatečnou hmotnost, aby jeho gravitace překonala vnitřní síly pevného tělesa (dosáhne kulového tvaru odpovídajícího hydrostatické rovnováze). 3) vyčistí okolí své dráhy od drobnějších těles. Planetami jsou Merkur, Venuše, Země, Mars, Jupiter, Saturn, Uran a Neptun. V poslední době se název planeta vžil i pro exoplanety obíhající kolem jiných hvězd, než je naše Slunce., kometyKometa – těleso malých rozměrů obíhající kolem Slunce většinou po protažené eliptické dráze s periodou od několika let po tisíce roků. Při přiblížení ke Slunci se vypařuje část materiálu jádra a kometa vytváří komu a eventuálně ohon. Jde o pozůstatky materiálu z doby tvorby sluneční soustavy. Dnes se nacházejí v Oortově oblaku za hranicemi sluneční soustavy, ve vzdálenosti 20 000÷100 000 au. Některé komety pocházejí i z bližšího Kuiperova pásu. a planetkyPlanetka – nesprávně asteroid, malé těleso o rozměrech maximálně stovek kilometrů na samostatné dráze kolem Slunce. Nejvíce planetek se nachází v tzv. Hlavním pásu mezi drahami Marsu a Jupiteru. Obdobná tělesa jsou i v Kuiperově pásu za drahou Neptunu. hlavního pásuHlavní pás – pás planetek mezi drahami Marsu a Jupiteru. Největším tělesem je planetka Ceres (průměr 974 km) objevená v roce 1801. V roce 2005 překročil počet známých těles Hlavního pásu 100 000. Jejich úhrnná hmotnost je ale velmi malá. Existuje zde jen 16 těles s rozměry nad 240 km. se v naší sluneční soustavě nachází řada dalších kategorií objektů, mezi něž patří i TrojanéTrojané – obecný název pro tělesa nacházející se v Lagrangeových bodech L4 a L5 soustavy Slunce-planeta. V těchto bodech tělesa samostatně obíhají Slunce a vyrovnává se zde odstředivá síla vzniklá oběhem s přitažlivými silami planety a Slunce. Lagrangeovy body L4 a L5 se nacházejí na dráze planety kolem Slunce, a to 60° před planetou a 60° za planetou. Lagrangeův bod (L4 nebo L5), planeta a Slunce tvoří rovnostranný trojúhelník. Trojané jsou v rezonančním pohybu 1:1 s oběžným pohybem planety. Tělesa v libračním bodě L4 soustavy Jupiter – Slunce se někdy označují jako „Řekové“ a tělesa v bodě L5 jako „Trojané“. (viz např. AB 43/2011), skupinka asteroidů obíhajících Slunce před a za planetou Jupiter. Trojané, řádově tisíce planetek, se nacházejí v Lagrangeových bodechLagrangeovy body – pět bodů v sousedství dvou obíhajících hmotných těles, ve kterých je gravitační a odstředivá síla vyrovnána. Polohu těchto bodů poprvé vypočítal italsko-francouzský matematik Joseph-Louis Lagrange. Velmi výhodné je například umístění sond určených k pozorování vzdáleného vesmíru do Lagrangeova bodu L2 soustavy Země-Slunce, který je vzdálený od Země 1 500 000 km ve směru od Slunce (WMAP, Planck, Herschel). Naopak, do bodu L1 soustavy Země-Slunce se umísťují sondy určené pro monitorování Slunce (například SOHO). Lagrangeův bod L3 soustavy Země-Slunce leží opačné straně Slunce, nepatrně dále, než je oběžná dráha Země. Body L4 a L5 neleží na spojnici obou těles, ale tvoří s nimi rovnostranné trojúhelníky. L4 a L5 soustavy Jupiter-Slunce. Lze nalézt podobné chování elektronůElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932. v samotném atomuAtom – základní strukturní jednotka hmoty, jádro je složeno z neutronů a protonů, obaly z elektronů. Rozměry atomu jsou 10−10 m, rozměry jádra 10−14 m, hustota atomu je 1011 g·cm−3, hustota jádra 1014 g·cm−3. Elektrony nejsou v atomárnáím obalu lokalizovány, můžeme určit jen pravděpodobnosti jejich výskytu v tzv. orbitalech.? Na první pohled by se dalo odpovědět, že takovéto stabilní konfigurace nám v atomu kvantová mechanika neumožní. V AB 31/2008 jsme si ale již mohli přečíst o studiu Rydbergových atomůRydbergův atom – atom excitovaný do vysokého hlavního a vedlejšího kvantového čísla. Rydbergovy atomy jsou velmi citlivé na okolní elektrická a magnetická pole. Elektronová vlnová funkce může být u některých superpozic stavů těchto atomů aproximována klasickým pohybem elektronu po kružnici. Vysoce excitované atomy jsou pojmenovány podle švédského fyzika Johannese Roberta Rydberga (1854–1919)., prováděném týmy vědců z Riceovy univerzity v Texasu a Vídeňské univerzity. Rydbergovými atomy se nazývají atomy, které mají alespoň jeden elektron excitovaný do extrémně vysoké energetické hladiny. Proto je interakce mezi tímto elektronem a jádrem daleko slabší a rozdíly mezi kvantovou a klasickou mechanikou se v takovémto systému poněkud stírají. Pojďme se podívat, jaké analogie si můžeme dovolit při studiu gravitačníhoGravitační interakce – interakce působící na všechny částice bez výjimky. Má nekonečný dosah a její intenzita ubývá s kvadrátem vzdálenosti. Současnou teorií gravitace je obecná relativita publikovaná Albertem Einsteinem v roce 1915. Podle této teorie kolem sebe každé těleso zakřivuje prostor a čas a v tomto pokřiveném světě se tělesa pohybují po nejrovnějších možných drahách, tzv. geodetikách. Obecná relativita předpověděla řadu jevů, které z Newtonovy teorie gravitace nevyplývají. pole a chování elektronových balíků v atomárním obalu.
Obr. 1. Rydbergův atom. Zdroj: Universita ve Stuttgartu.
|
Rydbergův atom – atom excitovaný do vysokého hlavního a vedlejšího kvantového čísla. Rydbergovy atomy jsou velmi citlivé na okolní elektrická a magnetická pole. Elektronová vlnová funkce může být u některých superpozic stavů těchto atomů aproximována klasickým pohybem elektronu po kružnici. Vysoce excitované atomy jsou pojmenovány podle švédského fyzika Johannese Roberta Rydberga (1854–1919). Kvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí respektovat omezení kvantové mechaniky na současnou měřitelnost či neměřitelnost veličin. Například základní energetický stav atomu značíme symbolem |S>, vakuový stav symbolem |0>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně. Kvantový stav je zpravidla charakterizován sadou kvantových čísel a je matematicky vyjádřen tzv. vlnovou funkcí (prvkem Hilbertova prostoru stavů). Kvantové číslo, hlavní – značíme n, čísluje energii systému En. Hodnota energie závisí na průběhu potenciální energie. Energie je proto jinak kvantována ve vodíkovém atomu, jinak v harmonickém oscilátoru, kvantové jámě, atd. Kvantové číslo, vedlejší – značíme l, vyjadřuje maximální možnou projekci momentu hybnosti do nějaké osy v jednotkách redukované Planckovy konstanty. U atomu vodíku nabývá vedlejší kvantové číslo hodnot 0, 1, ... n–1. Časté je označování vedlejšího kvantového čísla písmeny s, p, d, f..., které odpovídají hodnotám 0, 1, 2, 3... Velikost momentu hybnosti (nikoli projekce) je dána vztahem L2 = l(l+1)ħ2. Kvantové číslo, magnetické – značíme m, čísluje projekci momentu hybnosti do libovolného směru. Ta může nabývat celistvých násobků Planckovy konstanty ħ, tedy Lk = mħ. |
Rydbergovy atomy
Energie vnějšího elektronuElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932. vodíkupodobných atomů, tj. atomů, které mají v neuzavřené slupce jeden elektron, je záporná a nepřímo úměrná kvadrátu hlavního kvantového číslaKvantové číslo, hlavní – značíme n, čísluje energii systému En. Hodnota energie závisí na průběhu potenciální energie. Energie je proto jinak kvantována ve vodíkovém atomu, jinak v harmonickém oscilátoru, kvantové jámě, atd.
En ~ −1/n2.
Nejnižší a tedy nejstabilnější je pro základní stav, kde je hlavní kvantové čísloKvantové číslo, hlavní – značíme n, čísluje energii systému En. Hodnota energie závisí na průběhu potenciální energie. Energie je proto jinak kvantována ve vodíkovém atomu, jinak v harmonickém oscilátoru, kvantové jámě, atd. n = 1. Pro vyšší excitované stavy tato energie roste a pro velmi vysoká n se blíží zleva k nule. Energie vysoce excitovaného elektronu sice roste, ale roste ke konečnému číslu (nule), zatímco nejpravděpodobnější vzdálenost výskytu elektronu od jádra roste k nekonečnu. Tuto analogii z gravitačního pole známe. PlanetaPlaneta – nebeské těleso, které: 1) obíhá okolo Slunce. 2) má dostatečnou hmotnost, aby jeho gravitace překonala vnitřní síly pevného tělesa (dosáhne kulového tvaru odpovídajícího hydrostatické rovnováze). 3) vyčistí okolí své dráhy od drobnějších těles. Planetami jsou Merkur, Venuše, Země, Mars, Jupiter, Saturn, Uran a Neptun. V poslední době se název planeta vžil i pro exoplanety obíhající kolem jiných hvězd, než je naše Slunce. vázaná gravitačně ke SlunciSlunce – nám nejbližší hvězda, tzv. hvězda hlavní posloupnosti, která se nachází ve vzdálenosti 149,6×106 km od Země. Jde o žhavou plazmatickou kouli s průměrem 1,392×106 km, teplotou na povrchu 5 780 K, teplotou v centru přibližně 15×106 K a zářivým výkonem 3,846×1026 W. Zdrojem energie je jaderná syntéza, při které se za každou sekundu sloučí v jádru Slunce 700 milionů tun vodíku na hélium. má celkovou mechanickou energii zápornou. Čím více se energie planety blíží k nule (směrem od záporných hodnot, tím je poloosa trajektorie planety větší a v případě nulové celkové energie se trajektorie stává parabolou a oběžnice uniká do nekonečna. Proto nás nepřekvapí, že v případě Rydbergových atomůRydbergův atom – atom excitovaný do vysokého hlavního a vedlejšího kvantového čísla. Rydbergovy atomy jsou velmi citlivé na okolní elektrická a magnetická pole. Elektronová vlnová funkce může být u některých superpozic stavů těchto atomů aproximována klasickým pohybem elektronu po kružnici. Vysoce excitované atomy jsou pojmenovány podle švédského fyzika Johannese Roberta Rydberga (1854–1919). je elektron velice citlivý na vnější elektromagnetické pole a atom se může snadno ionizovat, tedy tento elektron s vysokým hlavním kvantovým číslem n zcela ztratit. Povšimněme si také, že rozdíl dvou sousedních hladin pro vysoká n se blíží k nule, a proto jsou přechody mezi takovýmito hladinami velmi snadné.
Analogie mezi planetárním modelem a elektronovým obalem přeci jenom pokulhává. Hlavní příčina je v kvantové mechanice, která například nedovoluje libovolné energie, ale jen diskrétní (nespojité) hodnoty, jak je patrné ze vztahu uvedeného výše. Rovněž tak moment hybnosti elektronu nemůže být libovolný, ale je kvantovaný. Podle Bohrových představ by měly být povoleny pouze takové trajektorie, jejichž obvod je celočíselným násobkem vlnové délky elektronu, tj.
2πrn = nλ.
Dalším podstatným rozdílem je fakt, že trajektorie planety okolo Slunce je vždy rovinná, zatímco elektron se může vyskytovat ve všech třech základních směrech. Přesto se pojďme podívat na paralelu mezi elektronemElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932. a planetouPlaneta – nebeské těleso, které: 1) obíhá okolo Slunce. 2) má dostatečnou hmotnost, aby jeho gravitace překonala vnitřní síly pevného tělesa (dosáhne kulového tvaru odpovídajícího hydrostatické rovnováze). 3) vyčistí okolí své dráhy od drobnějších těles. Planetami jsou Merkur, Venuše, Země, Mars, Jupiter, Saturn, Uran a Neptun. V poslední době se název planeta vžil i pro exoplanety obíhající kolem jiných hvězd, než je naše Slunce. blíže.
Paralela mezi elektronem a planetou
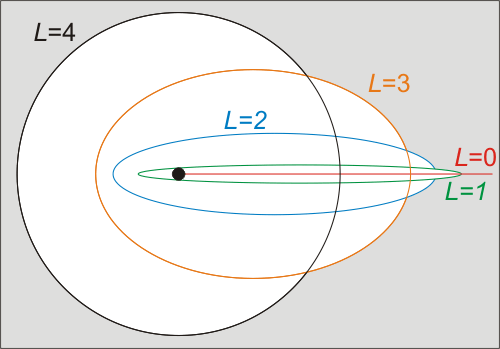
Obr. 2. Trajektorie s různým momentem hybnosti.
Na obrázku 2 jsou trajektorie planet s různým momentem hybnosti L (hodnoty jsou bezrozměrné). Představme si, že všechny planety mají stejnou celkovou mechanickou energii, tj. součet kinetické a potenciální energie. Liší se pouze velikostí tečné složky rychlosti v místě nejvíce napravo každé z elips, to znamená, že se liší velikostí momentu hybnosti L. V klasické fyzice by možnost, kdy je moment hybnosti roven nule, vedla k pádu do centra. To je ale v případě soustavy jádro – elektron nemožné, protože lokalizaci elektronu nekonečně blízko jádra vylučují Heisenbergovy relace neurčitostiRelace neurčitosti – v mikrosvětě není možné současně změřit polohu a hybnost objektů. Změření jedné veličiny naruší měření druhé veličiny. Čím přesněji zjistíme polohu, tím menší informaci budeme mít o hybnosti a naopak. Jde o principiální zákonitost kvantového světa, která souvisí s nekomutativností veličin na elementární úrovni. Relace neurčitosti objevil Werner Heisenberg. Stejné relace platí také mezi energií a časovým intervalem. Ve vakuu mohou po velmi krátkou dobu vznikat ve shodě s relacemi neurčitosti fluktuace (objekty) o určité energii. Čím vyšší energie, tím kratší doba života těchto fluktuací. Dále relace platí i pro jakoukoli zobecněnou souřadnici a její hybnost. Může jít například o nějaké pole, které nemůže mít současně nulovou hodnotu a nulovou hybnost, což vede k jeho vakuovým fluktuacím.
Δx Δp ≥ ħ/2.
Nulové velikosti momentu hybnosti odpovídají atomové orbitalyOrbital – oblast v atomárním či molekulárním obalu, kde se vyskytuje elektron. Pravděpodobnost výskytu elektronu v orbitalu je rovna druhé mocnině velikosti komplexní vlnové funkce. s, které jsou pro všechny energie (různá hlavní kvantová čísla n) kulově symetrické. Naopak čím větší je moment hybnosti, tím více se může tvar trajektorie blížit kružnici. (Až do případu, že má těleso právě kruhovou rychlost. Poté pak budou trajektorie opět elipsy a v případě vysoké rychlosti se trajektorie stane parabolickou, popřípadě hyperbolickou). Kvadrát momentu hybnosti lze pro soustavu atomové jádro – elektron vyjádřit ve tvaru
L2 = l(l + 1)ħ,
kde vedlejší kvantové číslo l nabývá hodnot 0,1,...n −1. Pro danou velikost momentu hybnosti, tedy l, může mít vlnová funkce elektronu různé tvary podle velikosti magnetického kvantového číslaKvantové číslo, magnetické – značíme m, čísluje projekci momentu hybnosti do libovolného směru. Ta může nabývat celistvých násobků Planckovy konstanty ħ, tedy Lk = mħ. m, které pro dané l nabývá hodnot −l, −l+1,…,l −1, l. Při vhodně zvoleném magnetickém kvantovém čísle ale můžeme sledovat jistou rovinnou symetrii vlnové funkce, která se při vysokých l začíná podobat kružnici. Na obrázcích jsou znázorněny vlnové funkce pro zvyšující se hlavní a vedlejší kvantová čísla n a l pro magnetická čísla m zvolená tak, aby vlnová funkce měla symetrii v rovině.
 |
 |
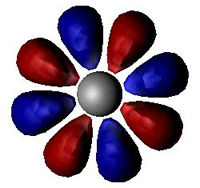 |
|
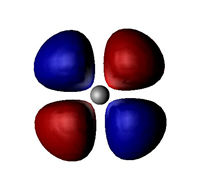
n = 3, l = 2 (orbital d) |
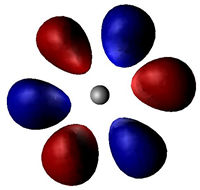
n = 4, l = 3 (orbital f) |
n = 5, l = 4 (orbital g) |
Obr. 3. Některé elektronové orbitalyOrbital – oblast v atomárním či molekulárním obalu, kde se vyskytuje elektron. Pravděpodobnost výskytu elektronu v orbitalu je rovna druhé mocnině velikosti komplexní vlnové funkce. (vykreslen je kvadrát velikosti vlnové funkce).
Kvadrát velikosti komplexní vlnové funkce udává pravděpodobnost výskytu elektronuElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932.. Pro skutečně vysoká n a l si můžeme podle obrázku 3 snadno představit, že elektron „bude někde na kružnici“ kolem atomového jádra.
Již zmíněný tým vědců ze Spojených států a Rakouska se pokoušel o lokalizaci elektronů na Rydbergových hladinách atomu draslíkuDraslík – Kalium, velmi důležitý a reaktivní prvek ze skupiny alkalických kovů, hojně zastoupený v zemské kůře, mořské vodě i živých organizmech. Draslík je měkký, lehký a stříbrolesklý kov, který lze krájet nožem. Volný kov se poprvé podařilo připravit roku 1807 siru Humphry Davymu.. Vědci se snažili vytvořit pravděpodobnostní oblak elektronu s kvantovým číslem n velikosti řádově stovek, který by obíhal jádro atomu podobně jako planeta. Matematicky je totiž možné vytvořit takovouto superpozici stavů, kdy se elektron bude chovat podobně jako oběžnice kolem Slunce. Problémem ale je, že se tato superpozice stavů v čase rychle rozpadá a otázkou bylo, zda a jak je možné tento křehký systém stabilizovat. Inspirace přišla právě z nebeské mechaniky, kde se na oběžné dráze o 60° před a za planetou JupiterJupiter – největší a nejhmotnější (1,9×1027 kg) planeta Sluneční soustavy má plynokapalný charakter a chemické složení podobné Slunci. Se svými mnoha měsíci se Jupiter podobá jakési „sluneční soustavě“ v malém. Jupiter má, stejně jako všechny obří planety, soustavu prstenců. Rychlá rotace Jupiteru (s periodou 10 hodin) způsobuje vydouvání rovníkových vrstev a vznik pestře zbarvených pásů. Charakteristickým útvarem Jupiterovy atmosféry je Velká rudá skvrna, která je pozorována po několik století. Atmosféra obsahuje kromě vodíku a helia také metan, amoniak a vodní páry. Teplota pod oblaky směrem ke středu roste. Na vrcholcích mraků je −160 °C, o 60 km hlouběji je přibližně stejná teplota jako na Zemi. Proudy tekoucí v nitru (v kovovém vodíku) vytvářejí kolem Jupiteru silné dipólové magnetické pole. nalézá relativně stabilní systém TrojanůTrojané – obecný název pro tělesa nacházející se v Lagrangeových bodech L4 a L5 soustavy Slunce-planeta. V těchto bodech tělesa samostatně obíhají Slunce a vyrovnává se zde odstředivá síla vzniklá oběhem s přitažlivými silami planety a Slunce. Lagrangeovy body L4 a L5 se nacházejí na dráze planety kolem Slunce, a to 60° před planetou a 60° za planetou. Lagrangeův bod (L4 nebo L5), planeta a Slunce tvoří rovnostranný trojúhelník. Trojané jsou v rezonančním pohybu 1:1 s oběžným pohybem planety. Tělesa v libračním bodě L4 soustavy Jupiter – Slunce se někdy označují jako „Řekové“ a tělesa v bodě L5 jako „Trojané“.. V atomovém obalu jádra ale není žádná taková těžká částice, kolem které by se vytvořila analogie Lagrangeových bodůLagrangeovy body – pět bodů v sousedství dvou obíhajících hmotných těles, ve kterých je gravitační a odstředivá síla vyrovnána. Polohu těchto bodů poprvé vypočítal italsko-francouzský matematik Joseph-Louis Lagrange. Velmi výhodné je například umístění sond určených k pozorování vzdáleného vesmíru do Lagrangeova bodu L2 soustavy Země-Slunce, který je vzdálený od Země 1 500 000 km ve směru od Slunce (WMAP, Planck, Herschel). Naopak, do bodu L1 soustavy Země-Slunce se umísťují sondy určené pro monitorování Slunce (například SOHO). Lagrangeův bod L3 soustavy Země-Slunce leží opačné straně Slunce, nepatrně dále, než je oběžná dráha Země. Body L4 a L5 neleží na spojnici obou těles, ale tvoří s nimi rovnostranné trojúhelníky.. Tuto „těžkou planetu“ však v experimentu nahradilo rotující elektromagnetické pole, které umožnilo realizovat lokalizované elektronové orbitalyOrbital – oblast v atomárním či molekulárním obalu, kde se vyskytuje elektron. Pravděpodobnost výskytu elektronu v orbitalu je rovna druhé mocnině velikosti komplexní vlnové funkce. a přemostit tak v tomto případě rozdíly mezi kvantovou a klasickou mechanikou. Vědci užili laser k excitaci osamělého elektronu v atomu draslíku na energii s hlavním kvantovým číslem okolo 300. Poté aplikovali lineárně polarizované sinusoidální pole, jehož frekvence byla v rezonanci s vlnovým balíkem a jehož fáze byla synchronizována s fází orbitalů, které zkombinovalo několik blízkých orbitalů a vytvořilo tak nedisperzní „trojanské vlnové balíky“. Elektron měl vysoce lokalizovanou vlnovou funkci, jejíž maximum pravděpodobnosti obíhalo po kruhové trajektorii.

Pracoviště na Riceově univerzitě. Student Shuzhen Ye
vytváří Rydbergův
atom za pomoci UV laseru. Zdroj: Riceova univerzita.
Navíc při citlivé změně frekvence tohoto polarizovanéhoPolarizace světla – jde o vlastnost, pomocí níž popisujeme určitou chaotičnost světla. Elektromagnetické záření je příčným vlněním, které lze ve vakuu popsat kmity vektorů E a B kolmých na sebe a na směr šíření vlny. U nepolarizované vlny opisují koncové body obou vektorů chaotické křivky. U polarizovaného světla je naproti tomu průmět obou vektorů do roviny kolmé na směr šíření vlny přesně definován. Podle tohoto průmětu pak rozlišujeme polarizaci rovinnou, kruhovou, a eliptickou. Polarizaci posuzujeme dohodou podle roviny kmitů elektrického vektoru. Při kruhové polarizaci opisuje konec elektrického vektoru v prostoru kružnici. Příkladem polarizovaného záření je například záření odražené od rovinného zrcadla. pole změní elektron svojí „dobu oběhu“, a dostane se tak na hladiny s vyšším kvantovým číslem. Ve výsledku se podařilo elektron vybudit na n okolo 600, a vytvořit tak atom draslíkuDraslík – Kalium, velmi důležitý a reaktivní prvek ze skupiny alkalických kovů, hojně zastoupený v zemské kůře, mořské vodě i živých organizmech. Draslík je měkký, lehký a stříbrolesklý kov, který lze krájet nožem. Volný kov se poprvé podařilo připravit roku 1807 siru Humphry Davymu. velikosti tečky nad písmenkem „i“.
Navzdory podobnosti mezi Trojany – asteroidy a trojanskými vlnovými balíky nám kvantová mechanika říká, že vlnový balík predikuje pouze pravděpodobnost nalezení elektronu v daném místě, zatímco klasická mechanika nám říká, kde přesně planetkaPlanetka – nesprávně asteroid, malé těleso o rozměrech maximálně stovek kilometrů na samostatné dráze kolem Slunce. Nejvíce planetek se nachází v tzv. Hlavním pásu mezi drahami Marsu a Jupiteru. Obdobná tělesa jsou i v Kuiperově pásu za drahou Neptunu. bude. To, co vědci měřili, byla pravděpodobnost zjištění, že je jeden elektron v určitém místě. Pro ověření musel experimentální tým z Riceovy univerzity provést mnoho a mnoho měření a porovnat svá zjištění s matematickým modelem teoretiků ve Vídni.
Praktické využití si, zdá se, nedokáží představit ani autoři článku, natož autor tohoto Bulletinu, nicméně již samotné studium oblastí na pomezí kvantové a klasické fyziky je nejenom zajímavé, ale také krásné. Tato oblast je plná fascinujících hádanek a ještě překvapivějších odpovědí.
Odkazy
