Kosmologie | Inflační vesmír

První inflační scénář

V roce 1979 si americký teoretik Alan Guth uvědomil, že určitým lékem na některé problémy standardního modelu by mohla být krátká překotná expanze v nejranější fázi existence vesmíru. Pokud by se někdy těsně po svém vzniku vesmír krátce exponenciálně nafoukl rozměrově o mnoho řádů, vyřešilo by to problémy horizontu a plochosti vesmíru, neexistence magnetických monopólůMagnetický monopól – neexistující analogie elektrického náboje v magnetickém poli. Dodnes není zcela jasné, proč se magnetické monopóly v přírodě nevyskytují. a pravděpodobně i problém počáteční singularity, neboť novou nulou by se stal počátek inflační fáze, při němž se vesmír zrodil z nějaké jiné předchozí podoby (často se uvažuje o kvantové pěně plné divokých fluktuací, které jsou důsledkem Heisenbergových relací neurčitostiRelace neurčitosti – v mikrosvětě není možné současně změřit polohu a hybnost objektů. Změření jedné veličiny naruší měření druhé veličiny. Čím přesněji zjistíme polohu, tím menší informaci budeme mít o hybnosti a naopak. Jde o principiální zákonitost kvantového světa, která souvisí s nekomutativností veličin na elementární úrovni. Relace neurčitosti objevil Werner Heisenberg. Stejné relace platí také mezi energií a časovým intervalem. Ve vakuu mohou po velmi krátkou dobu vznikat ve shodě s relacemi neurčitosti fluktuace (objekty) o určité energii. Čím vyšší energie, tím kratší doba života těchto fluktuací. Dále relace platí i pro jakoukoli zobecněnou souřadnici a její hybnost. Může jít například o nějaké pole, které nemůže mít současně nulovou hodnotu a nulovou hybnost, což vede k jeho vakuovým fluktuacím.). Vznik vesmíru je v inflačním modelu vlastně „pouhým“ fázovým přechodem z jednoho „skupenství“ do druhého. Dnes známe řadu teoretických i experimentálních faktů, které myšlenku inflace podporují, nicméně s jistotou její existence dokázána není. V průběhu inflace by podle výpočtů měly vzniknout tzv. reliktní gravitační vlny. Jejich polapení je velkou výzvou a mohlo by pomoci pochopit mechanizmus vzniku vesmíru (reliktní gravitační vlny jiného spektra by měly vzniknout i při jiném způsobu geneze vesmíru, například podle ekpyrotického scénáře).

Nejpravděpodobnějším důvodem inflační fáze bylo spontánní narušení GUTGUT – Grand Unified Theory, teorie velkého sjednocení. Popisuje sjednocení elektroslabé a silné interakce při energiích 10¹⁶ GeV (GUT škála). Při vyšších energiích než 10¹⁶ GeV existovaly pouze GUT interakce a gravitační interakce. Teorie velkého sjednocení předpovídá zatím nepozorované procesy, jako je například rozpad protonu. symetrie a následné oddělení silné interakce od elektroslabé při energii kolem 10¹⁴ GeV (tomu odpovídá čas 10⁻³⁵ s od nuly dané extrapolací expanze do počáteční singularity a teplota 10²⁷ K). Změna vlastností našeho vesmíru při této teplotě připomíná fázové přechody druhého druhu. Jako příklad lze uvést přechod feromagnetika přes Curieovu teplotu. Při teplotách T < T_c existují ve feromagnetiku Weissovy domény s orientovanými magnetickými momenty, a tím feromagnetické vlastnosti. Při teplotách T > T_c jsou magnetické momenty uspořádány chaoticky a materiál nemá makroskopické magnetické vlastnosti. Také v našem vesmíru při ochlazování pod teplotu T_c = T_GUT = 10²⁷ K došlo k prudké změně vlastností vesmíru a možná k nějakému typu fázového přechodu. Průběh potenciálu pole φ (může jít o analogii Higgsova pole či nějaké jiné pole zodpovědné za inflaci), které způsobují narušení symetrie, se s klesající teplotou vesmíru výrazně mění. Alan Guth ve své prvotní vizi navrhoval potenciál se dvěma minimy dle následujícího obrázku:

V počátečních fázích, při vysoké teplotě vesmíru, mělo inflační pole jediné energetické minimum pro hodnotu pole φ = 0. Vesmír tedy vznikl s touto nejnižší hodnotou energie inflačního pole. Jak se vesmír rozpínal a postupně chladl, objevilo se sekundární minimum energie s hodnotou φ = σ. Energie vakua tak už nemá nejnižší možnou hodnotu (hovoříme o „falešném“ vakuu). Při teplotě T < T_c dojde k fázovému přechodu, podobně jako tyto přechody známe u laboratorních materiálů. Fázový přechod nemusí nutně nastat při T = T_c, ale i později, vesmír se chová jako podchlazená kapalina, u které ještě nedošlo ke krystalizaci. Energetický rozdíl obou minim se odhaduje na ΔE ≈ (k_BT_c)⁴ ≈10⁵⁶÷10⁶⁰ GeV. V průběhu fázového přechodu, který by měl trvat cca 10⁻³⁷ s, se tato energie uvolní, dojde k ohřevu vesmíru téměř zpět na T_c, k zvýšení entropie faktorem 10⁸⁰ až 10⁹⁰ a k zvětšení rozměrů faktorem 10²⁰ až 10³⁰. Expanzní funkce se mění podle exponenciální závislosti a(t) = exp[χt]. Inflační pole se popisuje komplexní funkcí, na obrázku je na vodorovné ose zakreslena jen reálná část. Ve skutečnosti by ve vodorovném směru byly dvě osy (reálná a imaginární) a sekundární minimum by tvořilo celé údolí. Pole si z nekonečně hodnot vybere při fázovém přechodu jednu konkrétní, čímž dojde k narušení symetrie. Fázové přechody s narušením symetrie známe i z běžného života. Máme-li vodu, kterou postupně ochlazujeme, krystalizuje v pevnou fázi – led. Přitom fáze při vyšší teplotě měla vyšší symetrii (sférickou), fáze při nižší teplotě má nižší symetrii (například diskrétní symetrii ve směru krystalových rovin). V teoretických modelech jsou tyto fázové přechody doprovázeny vznikem různých topologických defektů:

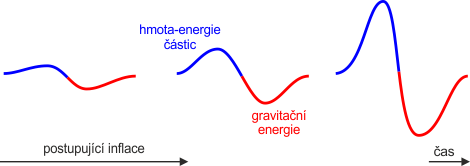
V průběhu inflace se vytváří značné množství částic na úkor prohlubující se záporné gravitační energie. Hmota těchto částic je tak vytvářena na dlouhodobý „dluh“ gravitační energii. Tento dluh bude možná splacen v závěrečných fázích vývoje vesmíru. Díky překotné tvorbě částic při inflaci zůstává hustota hmoty-energie částic při této expanzi konstantní.

Řešení problémů

Inflační model elegantně řeší oba dva základní problémy standardního modelu: problém plochosti vesmíru i problém horizontu. Připomeňme si ještě jednou Einsteinovu-Fridmanovu rovnici pro expanzní funkci (viz kapitola standardní model)

H ² − (8/3)πGρ = −c²k/a²;       H ≡ (da/dt)/a.

Čitatel i jmenovatel se v prvním členu chovají exponenciálně a exponenciální závislost se zkrátí. V druhém členu se exponenciální závislost výrazně neprojeví. Člen na pravé straně bude inflací ovlivněn zcela dominantně. Ve jmenovateli se objeví faktor exp[2χt], který způsobí zmenšení tohoto členu v průběhu inflační fáze. Pro další rozbor uvažujme například, že exp[2χt] ~10⁵⁸. Efektivní křivost vesmíru tak bude v průběhu inflační fáze nastavena téměř na nulu. Bezprostředně po inflaci bude ρ/ρ_c ≈ 1±10⁻⁵⁸ a v dnešní době ρ/ρ_c ≈ 1±10⁻⁶. Problém plochosti vesmíru je tak řešen nastavením vesmíru na kritickou hustotu v průběhu inflační fáze.

Před inflační fází byly pro náš příklad rozměry vesmíru 10⁵⁸krát menší než po jejím ukončení. To ale znamená, že rozměry vesmíru před inflační fází byly menší než horizont částic a že všechny oblasti byly kauzálně spojeny. Dokonce celý dnešní pozorovatelný vesmír byl v čase t_GUT v jediném světelném kuželu. To je způsobeno tím, že horizont částic narůstá lineárně s časem i v průběhu inflační fáze.

V průběhu inflační fáze dochází také k „vyhlazení“ vlivu některých typů počátečních podmínek. Podobně jako na nafukujícím se míči zmizí nerovnosti povrchu, zmizí vliv chaotických počátečních podmínek na budoucí podobu vesmíru (ne však všech typů). Dalším zajímavým efektem je „tvorba hmoty“. V inflační fázi zůstává zachována hustota energie před inflací. Zvětší-li se objem vesmíru, zvětší se ve stejném poměru i záporná gravitační energie a kladná hmotnost materiálních částic. Jakoby z ničeho se tvoří hmota, a přesto se nemění celková energie (součet gravitační potenciální energie a energie hmotnosti částic) ani její hustota. Inflační scénář řeší i některé další problémy standardního modelu. Za všechny připomeňme ještě problém neexistence magnetických monopólů. Ty by měly vzniknout v dosti značném množství jako topologické defekty při narušení GUTGUT – Grand Unified Theory, teorie velkého sjednocení. Popisuje sjednocení elektroslabé a silné interakce při energiích 10¹⁶ GeV (GUT škála). Při vyšších energiích než 10¹⁶ GeV existovaly pouze GUT interakce a gravitační interakce. Teorie velkého sjednocení předpovídá zatím nepozorované procesy, jako je například rozpad protonu. symetrie. Jestliže však proběhla inflační fáze a celý dnešní vesmír se v čase t_GUT nacházel v jediném světelném kuželu, může být v celém vesmíru monopólů jen několik.

Nový inflační scénář

Jak to tak bývá, inflační model řeší některé problémy standardního kosmologického modelu a přitom přináší jiné. Podle standardního inflačního scénáře došlo k přechodu ze stavu falešného vakua do stavu s nejnižší energií kvantovým tunelovým jevem. „Nová fáze“ vesmíru vznikala v různých místech vesmíru a šířila se v podobě jakýchsi bublin, které se postupně propojovaly. Charakter inflačního potenciálu vyžaduje tunelování potenciálovou bariérou. V průběhu tohoto procesu by ve vesmíru vznikalo veliké množství bublin nové fáze, které by se obtížně propojovaly a výsledkem by byl silně nehomogenní vesmír. Proto v roce 1982 navrhli Andrej Linde, Paul Steinhardt a Andreas Albrecht nový inflační scénář. Je založen na jiném průběhu potenciální energie inflačního  pole (na tzv. Colemanově-Weinbergově potenciálu. Tento potenciál má potenciálovou bariéru velmi plochou a dokonce při T → 0 tato bariéra vymizí. Podle nového scénáře mohlo vzniknout bublin nové fáze jen několik nebo jen jedna jediná.

Umělecká vize bublin nové fáze. Co bublina, to samostatným vesmír. Zdroj: MIT.

V dnešní době se intenzivně zkoumají možnosti vzniku inflační fáze bez fázového přechodu, inflační fáze s chaotickými počátečními podmínkami, možnosti inflace v jiných časech, než je t_GUT (například přímo v Planckově časePlanckovy škály – charakteristické rozměry získané kombinací fundamentálních konstant (gravitační, Planckovy a rychlosti světla). Planckova délka vychází 10⁻³⁵ m, Planckův čas 10⁻⁴³ s, Planckova hmotnost 10⁻⁸ kg a Planckova energie 10¹⁹ GeV., tj. v t_SUSY) nebo i existence několika inflačních fází a fázových přechodů v průběhu vývoje vesmíru (při každém narušení symetrie). V roce 1986 dokázal Andrej Linde, že k inflaci může dojít v bezprostředních okamžicích po Velkém třesku, jsou-li zde přítomna pole s kvadratickou závislostí potenciální energie na velikosti pole (tzv. inflatonová pole, V = mφ²/2). K nastartování inflace postačí, je-li počáteční hodnota pole větší než trojnásobek Planckovy hmotnosti. Je-li nenulová kosmologická konstantaKosmologická konstanta – člen v Einsteinových rovnicích obecné relativity, který je úměrný metrickému tenzoru (Λg_μν). Albert Einstein ho zavedl v roce 1917. Jeho účelem bylo, aby rovnice poskytovaly stacionární řešení. Po objevu expanze vesmíru v roce 1929 se tento člen jevil jako zbytečný. Moderní kosmologie o něm opět uvažuje v souvislosti s popisem zrychlené expanze vesmíru. Hodnota Λ odhaduje na Λ ~ 2×10⁻⁵² m⁻²., probíhá vývoj vesmíru ve třech fázích:

I.	exp [χt]	Lindeho inflace
II.	t2/3, t1/2	Fridmanova expanze
III.	exp [(Λ/3)1/2t]	De Sitterova inflace

Na počátku je klasická inflační fáze následovaná standardním Fridmanovým rozpínáním vesmíru s dominancí záření a později látky. Po dostatečném zředění vesmíru začne dominovat člen s kosmologickou konstantou. Vesmír se začne chovat jako prázdný (de Sitterův) vesmír s exponenciální expanzí způsobenou kosmologickým členem. V průběhu inflace se samozřejmě vůči sobě jednotlivé objekty pohybují nadsvětelnou rychlostí. Nejde o porušení principu relativity. Mezi takovými oblastmi nelze vyslat světelný paprsek, jsou kauzálně nespojené a žádná informace se mezi nimi nepřenáší. Lokálně samozřejmě může každý objekt komunikovat se svým bezprostředním okolí (až do horizontu) podsvětelnou rychlostí.

Co bylo, když nic nebylo

Dosti často se dnes také hovoří o stavu vesmíru před Velkým třeskem. Pokud taková otázka má vůbec smysl, znamená to do popisu vesmíru zapojit i kvantovou teorii pole, protože v počátečních fázích měly na vývoj vesmíru rozhodující vliv všechny 4 interakce. Ukazuje se, že potom není bezprostředně nutná divergence klasických veličin (hustota, teplota, křivost, Hubblova konstanta) v počátečním čase. Čas t = 0 lze chápat spíše jako okamžik maximální křivosti vesmíru. Také existuje druhá možnost, o které jsme se už zmínili, že skutečným počátečním časem je nástup inflační fáze.

Před inflací je vesmír ovládán zákony kvantové mechaniky (tzv. Wheelerovou-de Wittovou rovnicí). Jde o bezčasový kvantový stav bez klasických vlastností. V průběhu inflace dojde k dekoherenci – nevratné interakci kvantového subsystému s přirozeným okolím, která vede k objevení se klasických vlastností. V teoretických pokusech o spojení všech 4 interakcí (například strunovéStruny – jednodimenzionální útvary ve vícerozměrném světě (uzavřené nebo otevřené), jejichž vibrační stavy odpovídají jednotlivým elementárním částicím. Jde o podstatný prvek tzv. strunových teorií, které se pokoušejí spojit svět kvantové teorie se zakřiveným prostoročasem obecné relativity. teorie se supersymetriíSUSY – SUSY (SUper SYmmetry), supersymetrie, symetrie mezi fermiony a bosony, která by se měla projevovat při vysokých energiích. Ke každému fermionu by měl existovat superpartner, který je bosonem, a naopak ke každému bosonu by měl existovat superpartner, který je fermionem. Názvy superpartnerů tvoříme příponou „ino" pro bosony a předponou „s“ pro fermiony. Tedy například foton – fotino, elektron – selektron. Přestože se tyto superpartnery zatím nepodařilo experimentálně pozorovat na urychlovači LHC, představuje supersymetrie významnou ingredienci v teorii superstrun.) se vyskytuje většinou nové skalární pole – tzv. dilatonové pole, které je také schopné způsobit inflaci. Kosmologie založená na teorii strun se zpravidla nazývá strunová kosmologie. Do jaké míry odpovídá realitě, je ale nejasné.

Vícerozměrný vesmír strunové teorie, který by zde měl být přítomen v raných fázích, obsahuje méněrozměrné útvary, kterým říkáme D brány (D-branes, Dirichlet branes). Jde o nelokální časoprostorové defekty, které vytvářejí diskrétní buněčnou strukturu časoprostoru. Na těchto „bránách“ jsou lokalizována kalibrační a ostatní pole. Jediná gravitace je objemová a působí v celém vícerozměrném prostoru. Vytvářejí ji brány deformací Minkowského metriky. Brány mohou být také příčinou inflace. Brány se mohou překrývat a interagovat pomocí strun, jejichž otevřené konce jsou lokalizovány na membránách. Tímto mechanizmem vzniká nekomutativní geometrie časoprostoru, předpokládá se na škálách 10⁻²⁸ m. Brány mohou být zodpovědné dokonce za celý vznik vesmíru, a to bez inflační fáze. Jeden takový scénář se nazývá ekpyrotický model. Je založený na náhodném doteku dvou brán. Navrhli ho v roce 2001 Neil Turok, Paul Steinhardt, Burt Ovrut a Justin Khoury jako alternativu k inflačnímu modelu. Přítomnost brán na Plankových škáláchPlanckovy škály – charakteristické rozměry získané kombinací fundamentálních konstant (gravitační, Planckovy a rychlosti světla). Planckova délka vychází 10⁻³⁵ m, Planckův čas 10⁻⁴³ s, Planckova hmotnost 10⁻⁸ kg a Planckova energie 10¹⁹ GeV. ovlivňuje šíření fotonů, a mělo by proto dojít k novému typu disperze nezávislé na frekvenci fotonů. Tento jev by měl být detekován ve vysoce energetických gama záblescích i u některých pozemských experimentů s kaonyKaon – mezon K, částice složená z jednoho kvarku a jednoho antikvarku. Jeden kvark/antikvark je z první generace (d či u) a druhý kvark/antikvark je podivný kvark s. Kaony v hojné míře vznikají v horních vrstvách atmosféry při její interakci s kosmickým zářením. s b kvarkem. Ekpyrotický model také předpovídá vznik reliktních gravitačních vln typického frekvenčního průběhu. Jiný strunový model předpovídá vznik mnoha vesmírů z jedné jediné prabrány. Další z modelů předpovídá vznik vesmíru z černé díry lokalizované v extradimenzích. Oč méně experimentálních dat máme k dispozici, o to větší máme fantazii. Jen experimenty rozhodnou, zda vůbec některý z těchto modelů alespoň zdánlivě odpovídá realitě.

Zrod multiverza z jedné prabrány. Jedna z mnoha vizí vzniku vesmíru.
Slovo „vize“ je zde plně namístě. Zdroj: MoonRunner Design.