|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Matematika a fyzika – překvapení aritmetické geometrie
Jakub Kast Novák
Matematická fyzika? Co to je?
V souladu s galileovským myšlením, totiž, že matematika jest jazykem přírody, je jedním z dominantních přístupů ve fyzice přístup matematický. A tím se otevírá pojmoslovné okénko, které si na úvod neodpustím. Teoretická fyzika je dogmatem vědeckého bádání, kdy se fyzikální jevy vysvětlují striktně pomocí matematicko-racionálních metod. Experiment v takovém případě slouží buď jako iniciátor takového výzkumu, či jako potvrzovací aparát. A pak je tu pojem fyziky matematické. Převážně starší ročníky fyziků chápou přívlastky „teoretická“ a „matematická“ synonymně, ovšem současným přístupem je kladení čím dále většího důrazu na jejich rozlišení. Místo toho, abych tu v rozvleklých ciceronských souvětích rozepisoval jednotlivé nuance a diference, tak uvedu legendu daných pojmů, ze kterých rozdíly vyplynou samy:
|
Teoretická fyzika – racionálně-matematické vysvětlení jednotlivých fyzikálních jevů a jejich predikce, možnost myšlenkových experimentů (například teorie relativity, kvantová teorie a pod.) Matematická fyzika – vývoj matematických metod pro potřeby fyziky bez nutnosti zkoumání jednotlivých fyzikálních jevů, absence myšlenkových experimentů (například diferenciální geometrie časoprostoru, matematické metody kvantové mechaniky). Fyzikální matematika – matematická oblast motivovaná fyzikálními problémy, ovšem fungující ve své čisté formě abstrahované od jevů fyzikální reality (například kvantová algebra, geometrie dláždění inspirovaná výzkumem krystalů a kvazikrystalů). |
Nyní, když jsme si prošli tímto bludištěm pojmů, zaměřme se na to, jak teorie čísel může souviset s fyzikou.
Aritmetická geometrie a fyzikální úvahy
Teorie čísel je matematickým oborem, ve kterém primárně nezkoumáme všelijaké složité algebraické struktury, ale za základní objekt zkoumání bereme čísla a souvislosti mezi nimi. Vzpomeňme si například na různé věty o prvočíslech. Ale jak nám ukazuje slavná velká Fermatova věta, důležitými otázkami teorie čísel jsou otázky řešitelnosti rovnic všelijak definovaných množinami čísel. A takovými problémy se zabývá jihokorejský matematik Minhyong Kim, který se věnuje tzv. aritmetické geometriiAritmetická geometrie – použití technik algebraické teorie pro řešení problémů teorie čísel.. Kim si všiml, že mezi určitými aritmetickými objekty a aspekty kvantové teorie poleKvantová teorie pole – popis interakce založený na kvantových principech, tj. na nekomutativnosti základních operací v mikrosvětě. Kvantová teorie pole nahrazuje silové působení polními částicemi. Tyto částice jsou virtuální a nikdy nemohou skončit v detektoru, působí jen mezi dvěma interagujícími částicemi. Jako první prototyp kvantové teorie pole se vyvinula ve 30. letech 20. století kvantová elektrodynamika, později se objevila teorie slabé a silné interakce. Jediná gravitace je popsána jinak – za pomoci obecné relativity. se vyskytuje analogická souvislost. Posléze začal budovat aritmetickou geometrii pomocí jazyka fyziky, i když jak sám říká „amatérsky a ad hoc“ [1]. Pojďme si jeho práci přečíst okem pozorného čtenáře detektivních příběhů a možná na konci odhalíme, že vrahem není zahradník, jak by se očekávalo, ale někdo úplně jiný. No, prostě objevíme něco překvapivého!

Minhyong Kim. Zdroj: Quanta Magazine.
Svůj článek „Arithmetic Gauge Theory: A Brief Introduction“ (česky Aritmetická kalibrační teorie: Stručný úvod) začíná na článek matematický poněkud neobvykle vysvětlením Fermatova principu. Už na tomto lze vidět, že je to článek matematika určený pro matematiky – Fermatův princip je něco, co každý fyzik, doufám, zná. Princip říká, že světlo se v prostoru mezi dvěma body šíří po takové dráze, aby doba tohoto pohybu nabyla extrémní hodnoty, přičemž obvykle se jedná o co „nejkratší možný čas“. Princip vlastně říká, proč se světlo ohýbá, ohyb je nutný pro minimalizaci doby letu světla.

Pierre de Fermat. Zdroj: Wikipedia.
V druhé části svého článku se věnuje diofantické geometrii, což je speciální typ aritmetické geometrieAritmetická geometrie – použití technik algebraické teorie pro řešení problémů teorie čísel. a přímo souvisí s tzv. diofantickými rovnicemi – polynomiálními rovnicemi, v nichž hodnoty proměnných nabývají jen celých čísel. Již přívlastek diofantický, odvozený od antického myslitele Diofanta (3. stol. n. l.), značí, že se jedná o problém značně starý. I přesto je problém současný – jedná je o jeden z tzv. Hilbertových problémů. Velká Fermatova věta, dokázaná teprve roku 1994 britským matematikem Andrewem Wilesem, je diofantický problém a údajně vedla diofantická úloha Paula Diraca k uvažování o antihmotě (legenda je srozumitelně popsaná ve wikipedickém článku o diofantických rovnicích, konkrétně v kapitole Úloha vedoucí na diofantickou rovnici).
Když nás zajímá celočíselné řešení, tak nás samozřejmě musí zajímat i řešení racionální, neboť racionální číslo není nic jiného, než číslo, které lze zapsat ve tvaru podílu dvou celých čísel. Ovšem s racionálními řešeními je obtíž. Chceme-li najít obecné řešení nějaké rovnice, tak nám velmi pomáhá, když lze najít symetrický geometrický vzor daného řešení. Představme si rovnici x2 + y2 = 1. Řešení v oboru reálných čísel má geometrický vzor v podobě kružnice (viz obrázek níže). Ovšem budeme-li hledat jen řešení v oboru racionálních čísel, dostaneme nahodile umístěné body na dané kružnici reálného řešení. To je pro závěry o obecném řešení problém. Co tím mám na mysli? Není těžké najít jedno racionální řešení dané rovnice, dokonce není problém najít mnoho z nich. Ovšem trable nastávají v případě, kdy se snažíme hovořit o všech možných racionálních řešeních, neboť takový závěr dle obecného matematického mínění vyžaduje obecný vzor opakování řešení.
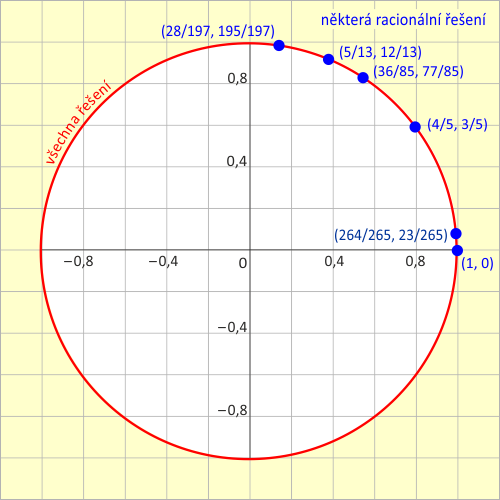
Řešení rovnice x2 + y2 = 1.
Červeně jsou reálná řešení, modře racionální řešení.
Zdroj: Quanta Magazine.
Zdá se, že abychom pochopili struktury racionálních řešení rovnice, bude vyžadován nový přístup. V současné době žijí hlavně dva pohledy na danou problematiku. O prvním z nich se zmíním jen okrajově, neboť pro matematickou fyzikuMatematická fyzika – vývoj matematických metod pro potřeby fyziky bez nutnosti zkoumání jednotlivých fyzikálních jevů, absence myšlenkových experimentů (například diferenciální geometrie časoprostoru, matematické metody kvantové mechaniky)., resp. fyzikální matematikuFyzikální matematika – matematická oblast motivovaná fyzikálními problémy, ovšem fungující ve své čisté formě abstrahované od jevů fyzikální reality (například kvantová algebra, geometrie dláždění inspirovaná výzkumem krystalů a kvazikrystalů)., se aktuálně nejedná o perspektivní oblast. Jedná se o rozlousknutí tzv. ABC domněnkyABC domněnka – též Oesterlého–Masserova domněnka. Mějme rovnici a + b = c. Čísla a, b jsou nestejná prvočísla. Domněnka říká, že součin různých prvočinitelů abc není „o mnoho“ menší než c., která souvisí s možnostmi řešení rovnice, během kterého japonský matematik Shinichi Mochizuki přišel s meziuniverzální Teichmüllerovou teorií. Není zde prostor pro její vysvětlení, on by to byl i problém – tato teorie není matematickou komunitou všeobecně přijímána pro její nesrozumitelnost.

Shinichi Mochizuki. Zdroj: Kjótská univerzita.
S druhým pohledem na problematiku racionálních řešení rovnic přišel právě Minhyong Kim. Jak jsem již předestřel, pro hledání obecností struktury se velmi hodí mít ve struktuře symetrie. Například český matematik Libor Barto zkoumá symetričnost problému ve vztahu k obecnému uchopení výpočetní složitosti a získal pro tento účel ERC grant. A pokud v aktuálním prostoru struktura žádné symetrie nemá, umístěme ji do prostoru, kde se již symetrie vyskytují. Takové umisťování zpravidla probíhá přes rozšíření původního prostoru. Myšlenka to není nová. Přišel s ní ve 40. letech minulého století francouzský matematik Claude Chabauty (mimo jiné člen slavné matematické skupiny Nicolas Bourbaki, která se snažila vybudovat celou matematiku na základě teorie množin), kdy zkonstruoval geometrický prostor pomocí tzv. p-adických číselp-adická čísla – běžným rozšířením racionálních jsou reálná čísla, resp. komplexní čísla. Ovšem p-adická čísla rozšiřují pro každé prvočíslo prostor prostřednictvím alternativního uchopení absolutní hodnoty – alternativně definuje pojem metriky, což je zobecnění pojmu vzdálenost., ve kterém racionální čísla tvoří vlastní symetrický podprostor. Tímto vlastně vzniknou dvě rovnice. Máme původní diofantickou rovnici, máme rovnici rozšířeného prostoru. Když zkonstruujeme grafy obou rovnic, tak v místech, kde se protínají, máme racionální řešení původní rovnice. Tento postup v 80. letech zdokonalil americký matematik Robert Frederick Coleman a po dlouhou dobu se jednalo o nejlepší nástroj pro hledání racionálních řešení diofantických rovnic. Problém tohoto řešení je, že body jsou často tak nahuštěny u sebe, že je nemožné určit řešení. Tudíž je zapotřebí přijít s metodou, která body více rozprostře v prostoru a umožní nám efektivnější řešení a hlavně řešení více druhů diofantických rovnic.
Pokud se chceme bavit o jakémsi exotickém rozšiřování prostoru, na které nepřišly dosud žádné hlavy pomazané, je dobré si říci, co je to vlastně prostor a zda by se jeho pojetí nedalo uchopit jinak. Matematický prostor, aby byl prostorem, musí splňovat určitou, přesně definovanou, geometrickou či topologickou strukturu. Když rozmístím libovolný počet bodů bez žádné zřejmé struktury, prostor nevytvořím. S takovým pojetím prostoru, mohu uvažovat o „soustavě prostorů“. Když si představím primitivní planimetrický útvar v podobě trojúhelníku, tak tento trojúhelník mohu rozsekat na další trojúhelníky a prostor tohoto trojúhelníku mohu rozšířit zase dalšími trojúhelníky.
Tato představa „prostoru prostorů“ je užitečná ve fyzikálním uvažování. Například v obecné relativitěObecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách. se časoprostor neustále vyvíjí a každý časoprostorový bod je dobré uvažovat v kontextu všech časoprostorových konfigurací. Dále se takové představy vyskytují v kalibračních teoriíchKalibrační teorie – teorie vystavěné na transformačních symetriích fyzikálních zákonů. Základním principem je doplňování symetrií do rovnic popisujících přírodní děje. Nové členy musí splňovat určité transformační vlastnosti. Tyto tzv. kalibrační transformace často vyžadují přítomnost nových kompenzujících polí, která nazýváme kalibračními poli. Kvanta kalibračních polí nazýváme kalibrační bosony. Žádná měřitelná veličina totiž nesmí záviset na výběru té či oné kalibrace, a to ani v klasické, ani v kvantové mechanice – příroda je kalibračně invariantní., které se zjednodušeně řečeno zabývají dynamikou polí a jak se tato pole během pohybu mění – opět se uvažuje více konfigurací polí naráz a pak se dá hovořit o jakémsi „prostoru všech polí“.
Různé fyzikální prostory se vyznačují symetriemi, které kladou důraz na různé body – spojnice mezi těmito body často představují v prostoru dráhu, po které je nutno se pohybovat, aby se minimalizoval čas. A nyní vidíme, proč Minhyong Kim na začátku své práce zdůrazňuje a vysvětluje Fermatův princip. Přemýšlí v analogii těchto bodů, které by ne ve fyzikálním, ale matematickém prostoru mohly znamenat racionální řešení diofantickcých rovnic. Rovnice definují křivky a jejich řešení vytváří prostor, který může mít i vyšší rozměry. Kim používá ve své práci trojrozměrný torus vykreslený rovnicí x4 + y4 = 1. Body racionálního řešení na tomto torusu postrádají strukturu, ale lze je přiřadit k bodům vyšších rozměrů než tři, které již strukturu mají. A přes toto přiřazení je možné hledat obecné řešení jednotlivých rovnic.
Jak taková konstrukce prostoru vyšších dimenzí probíhá? Jednoduše kreslí smyčky. Vytvoří se základní bod, což může být libovolný bod na toru. Pak se „nakreslí“ smyčka do libovolného jiného bodu. Pak postup opakuji, spojím základní bod s dalším jiným bodem a takto vlastně „osmyčkuji“ torus.
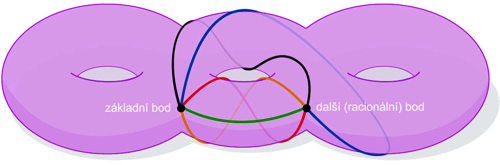
Konstrukce smyček a bodů. Zdroj: Quanta Magazine.
Je samozřejmé, že „osmyčkování“ záleží na volbě základního bodu. Každý základní bod bude mít jedinečný systém „osmyčkování“. Tím vzniká vlastně systém všech možných „osmyčkování“ a každý tento systém lze chápat jako bod ve vyšší dimenzi. A každý tento bod ve vyšší dimenzi lze přiřadit k základnímu bodu, ze kterého byl vytvořen, a začnou se vyskytovat symetrie, které se v trojrozměrné dimenzi nevyskytovaly a které mohou pomoci při obecném hledání racionálních řešení. Autor studie věří, že nalezení řešení leží v analogii s prostorem všech cest, kterým se paprsek světla může vydat. Jeho slovy ho čeká „nalezení principu nejmenšího působení v matematickém prostoru“.
Kim si dále všímá, že způsob, jakým se mění tento systém všech možných cest při pohybu z jednoho základního bodu do jiného, se silně podobá proměnlivosti pohybujícího se pole v kalibrační teoriiKalibrační teorie – teorie vystavěné na transformačních symetriích fyzikálních zákonů. Základním principem je doplňování symetrií do rovnic popisujících přírodní děje. Nové členy musí splňovat určité transformační vlastnosti. Tyto tzv. kalibrační transformace často vyžadují přítomnost nových kompenzujících polí, která nazýváme kalibračními poli. Kvanta kalibračních polí nazýváme kalibrační bosony. Žádná měřitelná veličina totiž nesmí záviset na výběru té či oné kalibrace, a to ani v klasické, ani v kvantové mechanice – příroda je kalibračně invariantní..
Závěr
Co jsem v článku předestřel, není fyzika. Je to matematika, ale silně ovlivněná fyzikálním uvažováním. Výzkum je stále v plenkách, ale je dost možné, že se před námi rodí zajímavá cesta řešení rovnic, kterou bude stát za to sledovat.
Odkazy
