|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Nízkoteplotná plazma II: Balada o voľnom elektróne alebo teória lavín
Vladimír Scholtz
Teória lavín, pomenovaná podľa Johna Sealy Townsenda, vysvetľuje základný samoudržiavací ionizačný mechanizmus elektrických výbojov. Prestavme si, že máme dve paralelné kovové dosky, medzi ktorými je dostatočne veľký objem plynu. Na doskách nech je napätie U a nech sa nám v tomto priestore z nejakého dôvodu náhodou objaví voľný elektrónElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932..
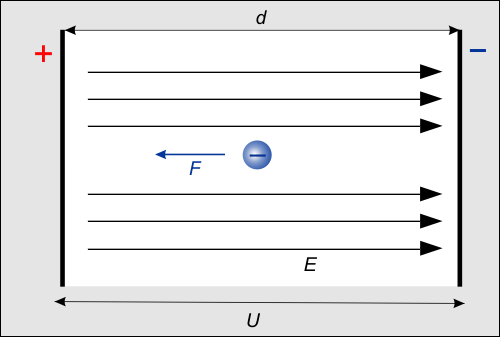
Obr. 1: Elektrón medzi kovovými doskami
|
Elektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932. Elektrický náboj – základní kvantový náboj elektromagnetické interakce. Elektrický náboj označujeme Q, jednotkou je coulomb (C). Nejmenším volným nábojem je náboj elektronu (1,6×10−19 C), jde o tzv. elementární náboj. Elektrické napětí – rozdíl elektrického potenciálu mezi dvěma místy, jde o elektrickou intenzitu sečtenou podél křivky mezi těmito body U = ∫E·dl. Napětí označujeme U, jednotkou je volt (V). Elektrický proud – elektrický náboj proteklý daným místem za jednotku času, I = dQ/dt. Elektrický proud označujeme I, jednotkou je ampér (A = C/s). |
Ak predpokladáme, že plyn medzi doskami je homogénny, že dosky sú rovnobežné, a že ich veľkosť je v porovnaní s ich vzdialenosťou d dostatočne veľká, môžeme povedať, že sa medzi nimi vytvorí homogénne elektrické pole E smerujúce od kladnej dosky (kladnej elektródy – anódy) k zápornej (zápornej elektróde – katóde), ktorého veľkosť sa rovná E = U/d. Toto elektrické pole pôsobí na voľný elektrón silou F = qE úmernou veľkosti elektrického poľa E a náboju elektrónu q = 1,602×10−19 C. Pôsobiaca sila urýchľuje elektrón (so zrýchlením a = F/me, kde me = 9.10938291×10−31 kg je hmotnosť elektrónu) a ten sa pohybuje v smere ku kladnej doske – anóde. Medzi doskami sú však neutrálne atómy alebo molekuly plynu a tak je vysoká pravdepodobnosť, že sa skôr alebo neskôr s nejakou určite zrazí.
Táto zrážka môže byť buď pružná, pri ktorej sa celková kinetická energia elektrónu a neutrálnej častice zachová a zmení sa iba smer ich pohybu, alebo nepružná, pri ktorej dôjde k odovzdaniu časti kinetickej energie elektrónu neutrálnej častici. V závislosti na konkrétnych podmienkach môže pri nepružnej zrážke dôjsť k excitácii alebo ionizácii neutrálnej molekuly. Pri exictácii sa časť kinetickej energie elektrónu odovzdá elektrónom neutrálnej častice, ktoré vystúpia na vyššie energetické hladiny, ale nedôjde ešte k ich odtrhnutiu. Pri ionizácii neutrálnej častice dôjde k ich vytrhnutiu a uvoľneniu elektrónu, čo má prakticky za následok vznik nového páru elektrón – kladný ión. Tento mechanizmus je charakterizovaný tzv. prvým Townsendovým koeficientom α, ktorý vyjadruje množstvo ionizačných zrážok jedného elektrónu na jednotku dĺžky. Rovnicou môžeme tento prírastok dN počtu voľných elektrónov N na dráhe dx vyjadriť ako
dN = α N dx.
Ak predpokladáme, že počiatočné množstvo voľných elektrónov je N0, dostávame ako riešenie rovnicu pre celkový počet elektrónov
N = N0 eαx.
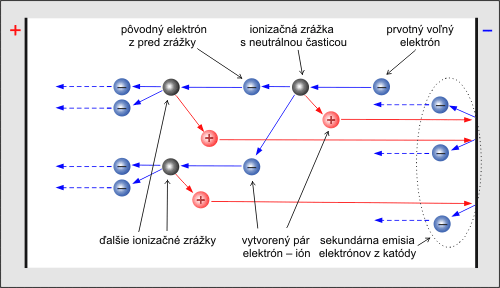
Pokiaľ je koeficient α > 1, vytvorí sa z jediného voľného elektrónu tzv. lavína a počet elektrónov stúpa exponenciálne s dráhou elektrónu. Počiatočný počet voľných elektrónov N0 je schopný na vzdialenosti d medzi elektródami ionizovať N − N0 neutrálnych častíc, z ktorých vzniknuté elektróny pokračovali na ceste k anóde a rovnaký počet vzniknutých kladných iónov sa vďaka svojmu opačnému elektrickému náboju pohyboval k elektróde zápornej, tj. ku katóde. Dopadom kladných iónov na katódu môže opäť dôjsť k pružným alebo nepružným zrážkam s atómami elektródy. Pravdepodobnosť vyrazenia voľného elektrónu vyjadruje tzv. druhý Townsendov koeficient sekundárnej emisie γ. Počet novo vyrazených elektrónov Nn z katódy je
Nn = γ (N0 eαd – N0).
Tieto voľné elektróny čaká rovnaký osud ako už bol popísaný pre voľný elektrón.
Obr. 2. Townsendova lavína.
Práve na základe týchto koeficientov je možné určiť, či bude počet elektrónov rásť alebo klesať. Rovnicu ešte môžeme upraviť na tvar
Nn = N0 γ(eαd –1),
kde práve výraz γ(eαd – 1) charakterizuje chovanie výboja. Pokiaľ je väčší ako jedna, bude počet elektrónov narastať a v medzielektródovom priestore sa začne formovať samostatný výboj. V opačnom prípade bude počet elektrónov klesať a výboj sa nezapáli. Podľa tejto rovnice by sa mal počet elektrónov medzi elektródami zväčšovať do nekonečna. V skutočnosti však ionizáciou vznikajúce páry elektrón – kladný ión vytvárajú opačné elektrické pole, ktoré znižuje celkovú hodnotu elektrického poľa medzi medzi elektródami, čím dochádza k znižovaniu koeficientov α aj γ až pokiaľ nedôjde k ustáleniu počtu voľných elektrónov.
|
John Sealy Townsend Anglický fyzik, ktorý sa zaoberal elektrickou vodivosťou plynov a kinetikou nabitých častíc v plynoch. Navrhol teóriu elektrónových lavín ako základný mechanizmus elektrických výbojov v plynoch. |
Klip týždňa
V klipu si môžete pozrieť vznik korónového výboja (a jemu podobných). Vzniká na rôznych predmetoch vo vysokofrekvenčnom poli s vysokým napätím. Výboj sa objaví v blízkosti ostrých hrotov, hrán nebo rohov, kde je elektrické pole najväčšie a ľahko vznikne lavína elektrónov. Zdroj: Youtube. (mp4, 22 MB)
Článok vznikol s podporou grantu ČVUT SGS10/266/OHK3/3T/13
Odkazy