Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 48 – vyšlo 16. prosince, ročník 9 (2011) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

48/2011

Je možné zviditelnit virtuální částice?

Miroslav Havránek

Skutečnost, že vakuum není zcela prázdný prostor, ale že se hemží páry virtuálních částic a antičástic, je známa téměř sto let. Virtuální částice nerespektují některé fyzikální zákony platné pro reálné částice (například Einsteinův vztah E²=p²c² + m²c⁴). Tyto částice žijí velmi krátce, nelze je přímo zachytit žádným přístrojem. Jejich přítomnost je ale možné prokázat několika způsoby. Jedním z nich jsou srážky částic na částicových urychlovačích, kde srážené částice interagují nejen mezi sebou, ale i s virtuálními částicemi z vakua. S těmito jevy fyzikové běžně počítají při výpočtech pravděpodobností různých fyzikálních procesů. Makroskopické projevy virtuálních částic je možné pozorovat jako statický Casimirův jevCasimirův jev – působení kvantového vakua na dvě blízké kovové rovnoběžné desky. Mezi deskami se mohou rozvinout fluktuace jen některých vlnových délek, mimo desky fluktuace libovolné vlnové délky. Výsledkem je přitažlivá síla působící na obě desky. Jev navrhli Hendrik Casimir a Dirk Polder. Experimentálně jev ověřili v roce 1948. nebo Lambův posuvLambův posuv – nepatrný posuv některých energetických hladin vodíku způsobený interakcí elektronu s vakuovými páry virtuálních částic. Tento posuv expermentálně změřili Willis Lamb a Robert Retherford v roce 1947.. Je ale možné vytrhnout virtuální částice ze spárů neúprosného vakua a přenést je do reálného světa? Odpověď na tuto otázku se pokusíme zodpovědět v dnešním bulletinu.

Obr. 1: Umělecká vize zařízení pro měření dynamického Casimirova jevu. Zdroj [3].

Virtuální částice – částice, které nepřetržitě vznikají a zanikají ve vakuu. Existenci virtuálních částic umožňují Heisenbergovy relace neurčitosti pro energii a čas. Virtuální částice také zprostředkovávají interakce mezi skutečnými částicemi a jsou zodpovědné za některé makroskopické jevy, jako je například anomální magnetický moment elektronu, Lambův posuv nebo Casimirův jev. Relace neurčitosti – v mikrosvětě není možné současně změřit polohu a hybnost objektů. Změření jedné veličiny naruší měření druhé veličiny. Čím přesněji zjistíme polohu, tím menší informaci budeme mít o hybnosti a naopak. Jde o principiální zákonitost kvantového světa, která souvisí s nekomutativností veličin na elementární úrovni. Relace neurčitosti objevil Werner Heisenberg. Stejné relace platí také mezi energií a časovým intervalem. Ve vakuu mohou po velmi krátkou dobu vznikat ve shodě s relacemi neurčitosti fluktuace (objekty) o určité energii. Čím vyšší energie, tím kratší doba života těchto fluktuací. Dále relace platí i pro jakoukoli zobecněnou souřadnici a její hybnost. Může jít například o nějaké pole, které nemůže mít současně nulovou hodnotu a nulovou hybnost, což vede k jeho vakuovým fluktuacím. SQUID – citlivý magnetometr, kterým se měří velmi slabá magnetická pole za pomoci supravodivé smyčky obsahující Josephsonův spoj. Zařízením lze změřit i extrémně slabá pole až do 5×10–18 T. Název zařízení je zkratkou z anglického „Superconducting Quantum Interference Device“. Samotné slovo „squid“ znamená v češtině krakatice (hlavonožec žijící v oceánech).

Dynamický Casimirův jev

Statická verze Casimirova jevu se projevuje jako nepatrná (avšak měřitelná) přitažlivá síla mezi dokonale hladkými rovnoběžnými zrcadly. Tato síla je důsledkem přítomnosti virtuálních fotonů – kvantových fluktuací elektromagnetického pole ve vakuu. Virtuální fotony tvoří mezi nehybnými zrcadly stojaté vlny. Přítomnost zrcadel nastavuje okrajové podmínky pro tyto vlny tak, že na povrchu zrcadel je elektrické pole rovné nule. To má za následek, že mezi zrcadly mohou vznikat pouze fotony určitých vlnových délek, zatímco vně zrcadel takové omezení neplatí. Tlak záření virtuálních fotonů z okolního prostředí tedy způsobuje přitažlivou sílu mezi zrcadly. Co se ale stane, pokud se zrcadla navzájem pohybují? Mění-li se vzdálenost mezi zrcadly, mění se i obrazec stojatých vln. Při nízkých rychlostech zrcadla se stojaté vlny dynamicky přizpůsobují měnícím se okrajovým podmínkám. Při rychlostech blížících se rychlosti světla se ale vlny už nestíhají přizpůsobovat, a dochází tak k emisi reálných (měřitelných) fotonůFoton – základní kvantum energie elektromagnetického záření, polní částice elektromagnetické interakce. Má nulovou klidovou hmotnost a nemá elektrický náboj. Jeho energie a hybnost jsou přímo úměrné frekvenci záření (E = ħω, p = E/c). Stav fotonu zahrnuje také polarizaci, protože jde o příčné vlnění. Kvantování energie poprvé zavedl Max Planck při pokusech o vysvětlení záření černého tělesa. Albert Einstein dal těmto kvantům reálný význam v roce 1905 při vysvětlení fotoelektrického jevu. Samotný název foton poprvé pro tuto částici použil až americký fyzikální chemik Gilbert Lewis v dopise časopisu Nature z roku 1926.. Tento proces se nazývá dynamický Casimirův jev. V minulosti proběhlo několik pokusů tyto fotony přímo měřit. Jedním z nejúspěšnějších byl nedávno publikovaný experiment skupiny vědců z Technické univerzity v Chalmers ve Švédsku, který popíšeme v následujícím odstavci.

SQUID – „kmitající zrcadlo“

Kdybychom kmitali se zrcadlem frekvencí 1 Hz s výchylkou 1 metr, pak bychom průměrně čekali na vyzáření jediného fotonu přibližně 22 miliard let. S využitím zrcadla na bázi nanomechanických oscilátorů se lze dostat na čekací dobu na jeden foton kolem dvaceti let. Existuje ale trik, kterým lze vyprodukovat za jedinou sekundu 100 000 Casimirových fotonů. Situaci analogickou kmitajícímu zrcadlu lze vytvořit v mikrovlnné oblasti spektra pomocí vlnovodu, jehož elektrická délka se velmi rychle mění v čase. Schéma takového zařízení pro měření dynamického Casimirova jevu je znázorněno na obrázku 2.

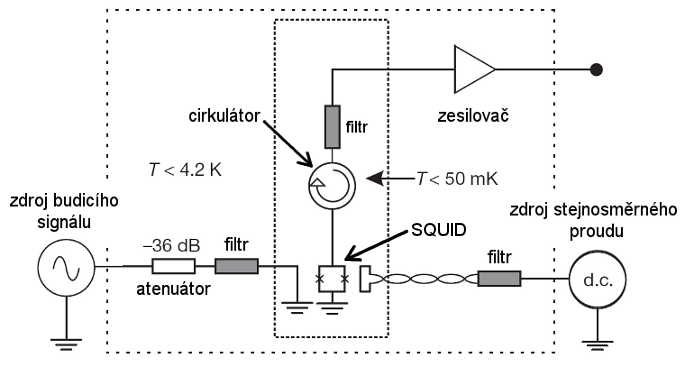
Obr. 2: Schéma experimentu pro měření dynamického Casimirova jevu. Vstupní budící signál moduluje indukčnost zařízení SQUID, a tím i elektrickou délku vedení. Záření produkované při dynamickém Casimirově jevu je zesíleno a dále zpracováno standardními elektronickými obvody.

Hlavní část přístroje představuje měřicí koplanární mikrovlnný vlnovod zakončený zařízením SQUIDSQUID – citlivý magnetometr, kterým se měří velmi slabá magnetická pole za pomoci supravodivé smyčky obsahující Josephsonův spoj. Zařízením lze změřit i extrémně slabá pole až do 5×10^–18 T. Název zařízení je zkratkou z anglického „Superconducting Quantum Interference Device“. Samotné slovo „squid“ znamená v češtině krakatice (hlavonožec žijící v oceánech)., který se chová na vysokých frekvencích jako indukčnost. Hodnotu indukčnosti lze velmi rychle modulovat vnějším magnetickým polem. V reálném experimentu je SQUID vystaven rychlým změnám magnetického toku generovaného budicím vlnovodem, který je zakončen zkratem ve vzdálenosti pouhých 20 μm od zařízení SQUID. Frekvence sinusového budicího signálu je 10,3 GHz. V blízkosti zařízení SQUID je také umístěn vodič, kterým protéká stejnosměrný elektrický proud generující konstantní magnetický tok, a nastavuje tak SQUID do pracovní oblasti s nejvyšší citlivostí a linearitou. Díky induktivní vazbě mezi SQUID a budicím vlnovodem dochází v rytmu vstupního signálu ke změnám indukčnosti modulu SQUID, a tím i ke změně elektrické délky vlnovodu. Tyto změny odpovídají urychlování zrcadla na rychlost rovnou čtvrtině rychlosti světla. Výstupní signál (projev dynamického Casimirova jevu) je pak odváděn měřicím vedením a přes cirkulátor k zesilovači. Jelikož se při experimentu měří signál nízké amplitudy o mikrovlnných frekvencích, je nutné aktivní část experimentu podchladit na teplotu 50 mK, čímž se eliminuje vliv tepelného záření. Dalšího omezení vlivu tepelného záření je docíleno pomocí filtrů na mikrovlnných vlnovodech. Podchlazení experimentu je důležité také pro správnou funkci zařízení SQUID.

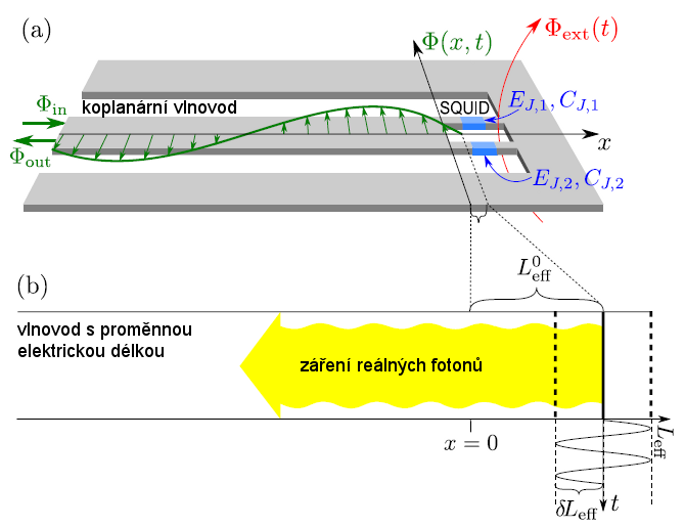
Obr. 3: Mikrovlnný vlnovod zakončený modulem SQUID ve vnějším magnetickém poli
je analogický vlnovodu s proměnnou elektrickou délkou. Zdroj [2]

Jak ale poznat, že pozorujeme právě dynamický Casimirův jev? Kvantová teorie předpovídá, že fotony dynamického Casimirova jevu vznikají v párech a jsou navzájem korelované. Součet frekvencí obou fotonů je roven frekvenci budicího signálu zařízení SQUID. Očekávané spektrum výstupního signálu by mělo být symetrické okolo poloviční frekvence budicího signálu. Záření těchto vlastností je proto nezaměnitelné s tepelným šumem. Na obrázku níže je znázorněno spektrum výstupního signálu jako funkce výkonu budicího signálu. Symetrie je zde velmi patrná. Prokázání korelace fotonů je složitější úkol. Zatím neexistuje detektor, který by umožňoval detekci jednotlivých fotonů v mikrovlnné oblasti, se kterým by bylo možné přímo měřit například časovou koincidenci nebo energii obou fotonů. Měřením kvadraturních složek výstupního signálu v horním a dolním pásmu okolo poloviny frekvence budicího signálu byl změřen stupeň korelace fotonů, který souhlasí s teoretickou předpovědí.

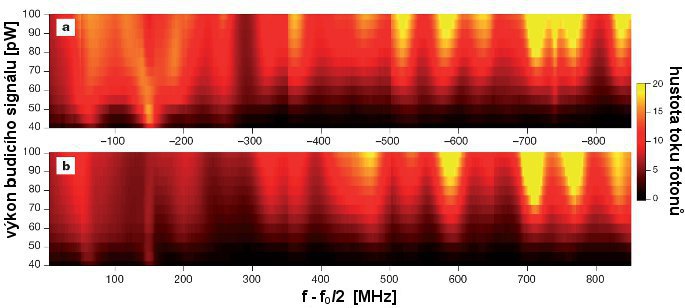
Spektrum výstupního signálu jako funkce výkonu budicího signálu. Symetrie okolo
frekvence budicího signálu f₀/2 je zde velmi patrná. Zdroj [1].

Závěr

Produkce reálných fotonů z vakua není „zadarmo“. Energie na jejich produkci pochází z kinetické energie zrcadla. Lze říci, že vakuum působí na urychlované zrcadlo brzdnou silou, která jej zpomaluje. Dynamický Casimirův jev není jediným možným způsobem, jak zviditelnit virtuální částice. Dalším příkladem může být vypařování černých děr, které teoreticky předpověděl Stephen Hawking v roce 1974. Pokud v blízkosti horizontu událostí černé díry vznikne pár virtuálních částic, přičemž se jedna z nich dostane pod horizont událostí, zbývající částice se stane reálnou, a tvoří tak Hawkingovo záření černé díry. Energie na vytvoření reálné částice pochází z černé díry, která se vypařováním postupně zmenšuje. Horizont událostí tedy také představuje okrajové podmínky pro kvantové fluktuace vakua a umožňuje tak virtuálním částicím stát se reálnými.

Odkazy