Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 16 – vyšlo 12. července, ročník 4 (2006) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

16/2006

Metamateriály

Petr Kulhánek

Tam, kde v bohatství přírody občas něco schází, si tu a tam člověk svým umem dopomůže sám. A někdy výsledky překvapí i samotné tvůrce. Nově se rodící odvětví metamateriálůMetamateriál – umělá struktura, která se v přírodě nevyskytuje a vykazuje atypické elektrické, magnetické a akustické vlastnosti, například permitivitu, permeabilitu, index lomu, akustickou propustnost a další. Vlastnosti metamateriálů bývají zpravidla silně závislé na frekvenci, takže výhodné vlastnosti pro určité technologie existují jen v úzkém pásmu frekvencí. je toho důkazem. Za metamateriály považujeme uměle vyrobené látky, které mají elektromagnetické vlastnosti v přírodě se nevyskytující.

Metamateriál – umělá struktura, která se v přírodě nevyskytuje a vykazuje atypické elektrické, magnetické a akustické vlastnosti, například permitivitu, permeabilitu, index lomu, akustickou propustnost a další. Vlastnosti metamateriálů bývají zpravidla silně závislé na frekvenci, takže výhodné vlastnosti pro určité technologie existují jen v úzkém pásmu frekvencí. LH materiál – prostředí, které vykazuje současně zápornou permitivitu a permeabilitu. Označení LH (Left Handed) znamená, že vektory k, E, B zde tvoří levotočivou ortogonální soustavu (v izotropním prostředí). Veselagova čočka – planparalelní destička se záporným indexem lomu, zobrazuje bod na bod. Teoreticky se jako první zabýval hypotetickým prostředím se záporným indexem lomu Victor Veselago v roce 1968. SRR – Split Ring Resonator, kruhový štěrbinový rezonátor. Základní součástka metamateriálů se zápornou permeabilitou navržená Johnem Pendrym z Imperial College London v roce 1999.

Záporná permitivita

Prostředí se zápornou permitivitouPermitivita – lineární koeficient úměrnosti mezi elektrickou indukcí a intenzitou. V izotropním a homogenním materiálu jde o jediné číslo, v komplikovanějších materiálech o tenzor (matici) koeficientů. (vektory D a E míří opačným směrem) je známo ve fyzice plazmatu relativně dlouho. Uměle ho lze vytvořit například pomocí soustavy paralelních drátků, kdy je permitivita dána jednoduchým rezonančním vztahem:

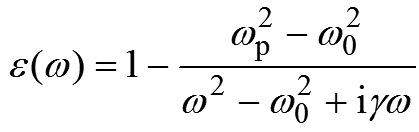
ve kterém jsou frekvence ω_p a ω₀ dány konfigurací pole drátků, γ je útlum a ω je frekvence dopadající elektromagnetické vlny. Jde o klasický rezonanční vztah známý například z teorie vybuzených kmitů. Ze vztahu je zřejmé, že permitivita má v okolí rezonance jak reálnou, tak imaginární část a reálná část je pro určitou oblast frekvencí záporná. Dopadající elektromagnetická vlna bude v oblasti rezonance absorbována a nebude prostředím procházet. Rozsáhlé pole drátků má vzhledem k vlně relativně izotropníIzotropní – stejný ve všech směrech. odezvu a je snadno zkonstruovatelné pro radiové i vyšší frekvence. Při dnešní úrovni nanotechnologiíNanotechnologie – obor zabývající se aplikováním výsledků nanofyziky. Zkoumá možnosti, jak vytvářet zařízení molekulových rozměrů a jak manipulovat s jednotlivými atomy tak, aby se dosáhlo žádaných vlastností. Protože u zařízení vyrobených pomocí nanotechnologie můžeme jejich činnost předurčit polohou a druhem jednotlivých atomů, můžeme dosáhnout maximální účinnosti, efektivity a výkonu, při dodržení malých rozměrů. a nanovláken nebude problém takové pole realizovat i v optické oblasti.

Záporná permeabilita

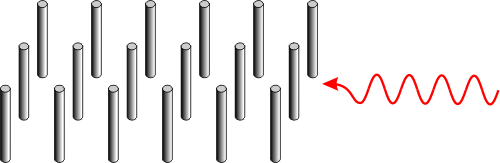
Vyrobit prostředí se zápornou permeabilitouPermeabilita – lineární koeficient úměrnosti mezi magnetickou indukcí a intenzitou. V izotropním a homogenním materiálu jde o jediné číslo, v komplikovanějších materiálech o tenzor (matici) koeficientů. je mnohem těžší. První návrh pochází od Johna Pendryho (Imperial College London) z roku 1999. Je složené z mnoha se opakujících štěrbinových rezonátorů (SRRSRR – Split Ring Resonator, kruhový štěrbinový rezonátor. Základní součástka metamateriálů se zápornou permeabilitou navržená Johnem Pendrym z Imperial College London v roce 1999.). V původním návrhu jde o dva koncentrické vodivé kroužky (vytvořené například z mědi), z nichž každý má štěrbinu na opačné straně. Kroužky jsou kapacitně i indukčně vázány. Elektromagnetická vlna dopadající kolmo na rezonátor v něm při rezonanci vybudí proud s jedním maximem tekoucí podél kroužků. Rezonátor se chová jako magnetický dipól s velmi intenzivní odezvou na elektromagnetickou vlnu. Samozřejmě jsou možné i vyšší rezonance na vyšších frekvencích s více maximy proudu tekoucího podél kroužků. Na opačných stranách každé štěrbiny se hromadí opačné elektrické náboje. Základní návrh rezonátoru SRRSRR – Split Ring Resonator, kruhový štěrbinový rezonátor. Základní součástka metamateriálů se zápornou permeabilitou navržená Johnem Pendrym z Imperial College London v roce 1999. (nalevo na obrázku) má při rezonanci i nenulový elektrický dipólový moment. Symetrické analogie (například rezonátor napravo) již mají elektrický dipólový moment nulový.

Různé varianty štěrbinového rezonátoru SRRSRR – Split Ring Resonator, kruhový štěrbinový rezonátor. Základní součástka metamateriálů se zápornou permeabilitou navržená Johnem Pendrym z Imperial College London v roce 1999.. Nalevo je nejčastější varianta navržená Pendrym.
Napravo je varianta mající nulový elektrický dipólový moment. Kresba autor.

Permeabilita soustavy štěrbinových rezonátorů je v okolí rezonance dána ještě jednodušším vztahem než permitivita soustavy drátků (je to tím, že neexistují magnetické náboje – monopóly). Imaginární část permeability vytváří klasický rezonanční pík, reálná část má v oblasti frekvencí těsně nad rezonancí výraznou zápornou hodnotu.

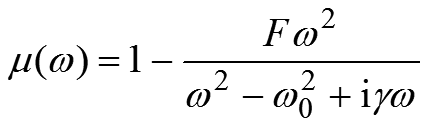
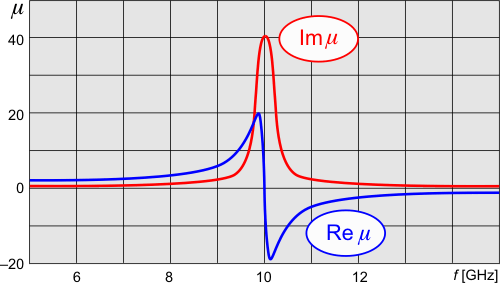
Permeabilita soustavy štěrbinových rezonátorů v oblasti rezonance.
Hodnoty platí pro smyšlené parametry rezonátoru. Kresba autor.

V oblasti rezonance je elektromagnetická vlna soustavou rezonátorů pohlcována. Rezonátory je možné stavět buď do dvourozměrných polí nebo do třírozměrných útvarů obdobných klasickým krystalům. Jen ve vrcholech mříže jsou namísto atomů jednotlivé rezonátory. Velikost rezonátorů může být v laboratorních podmínkách v centimetrech nebo v milimetrech, potom k rezonanci dochází na radiových vlnových délkách. V profesionálních laboratořích se ovšem již podařilo vyrobit pole napařených měděných rezonátorů o velikosti rezonátoru přibližně 50 mikrometrů. Zde je odezva rezonátorů v terahertzové oblasti. Jde o submilimetrové vlny, které například procházejí oděvy a dosud neexistoval přírodní materiál s intenzivní odezvou na tyto vlny. Takový materiál může být využit například v letištních skenerech při bezpečnostních kontrolách. V současnosti se vědci dostávají na hranici infračerveného oboru a intenzivně zkoumají, jak posunout rezonanci do viditelné oblasti.

Velikost rezonátorů v desítkách mikrometrů znamená jejich intenzivní odezvu v terahertzové oblasti a velkou aplikační budoucnost. Na fotografii jsou měděné štěrbinové rezonátory SRRSRR – Split Ring Resonator, kruhový štěrbinový rezonátor. Základní součástka metamateriálů se zápornou permeabilitou navržená Johnem Pendrym z Imperial College London v roce 1999. zobrazené řádkovacím elektronovým mikroskopem. Zdroj: U.S. Department of Energy Ames Laboratory).

Prostorové varianty štěrbinového rezonátoru.

Záporný index lomu

Prostředí se záporným indexem lomu zkonstruoval David R. Smith (University of California, San Diego) v roce 2000 pomocí kombinace pole drátků (se zápornou permitivitou) spolu s polem štěrbinových rezonátorů (se zápornou permeabilitou), které byly konstruovány tak, aby rezonance probíhala na stejné frekvenci. Je-li například permitivita a permeabilita rovna −1, můžeme psát:

Klíčové pro volbu komplexní větve odmocniny je to, že pro pasivní materiál musí mít druhá odmocnina permitivity i permeability kladnou imaginární část, jinak by docházelo k samovolnému zvětšování amplitudy. V případě oddělených polí elektrických a magnetických rezonátorů je elektromagnetická vlna absorbována, v případě jejich kombinace se v oblasti záporného indexu lomu objeví okno propustnosti a vlna prostředím se záporným indexem lomu prochází.

Kombinované pole drátků a štěrbinových rezonátorů v laboratořích. LH materiál v praxi.
Zdroj: Multitel, 2004 (nalevo), J. Pendry, D. Smith (napravo).

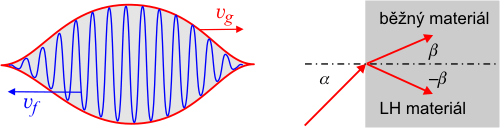
Nalevo: fázová a grupová rychlost v LH materiálu. Napravo lom v LH materiálu. Kresba autor.

Vlastnosti hypotetického materiálu se záporným indexem lomu teoreticky analyzoval již ruský vědec Victor Veselago v roce 1968. Takový materiál má zcela mimořádné chování. Magnetické vektory B a H míří opačným směrem, stejně tak elektrické E a D. Vektory k, E, B zde tvoří levotočivou ortogonální soustavu, hovoříme o tzv. LH materiáluLH materiál – prostředí, které vykazuje současně zápornou permitivitu a permeabilitu. Označení LH (Left Handed) znamená, že vektory k, E, B zde tvoří levotočivou ortogonální soustavu (v izotropním prostředí).. Poyntingův vektorPoyntingův vektor – vektor toku energie, S = E×H, jednotkou je W/m². určující směr přenosu energie míří na opačnou stranu než obvykle a grupová rychlost (ve směru přenosu energie) má proto opačný směr než fázová rychlost. Lom na rovinném rozhraní s LH materiálemLH materiál – prostředí, které vykazuje současně zápornou permitivitu a permeabilitu. Označení LH (Left Handed) znamená, že vektory k, E, B zde tvoří levotočivou ortogonální soustavu (v izotropním prostředí). probíhá na druhou stranu od kolmice než v běžném materiálu.

Veselagova čočka

Rovinná deska z LH materiálu by fungovala jako spojná čočka. A ne ledajaká čočka. Ohnisková vzdálenost by se mohla měnit pouhou změnou polohy předmětu. Žádné zakřivené plochy, žádná kulová vada. Žádné omezení rozlišovací schopnosti na vlnovou délku použitého elektromagnetického záření. A procházející vlna dokonce není exponenciálně tlumená jako u spojky. Zkrátka perfektní čočka.

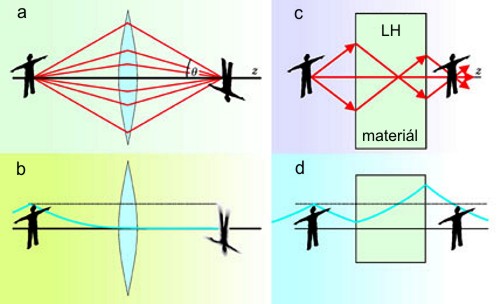
Porovnání klasické a Veselagovy čočky. (a) Klasická čočka potřebuje k dobrému rozlišení velkou aperturuApertura – využitelný průměr čočky objektivu, primárního zrcadla dalekohledu nebo jiného optického zařízení., aby byla schopna lámat i paprsky pod velkým úhlem. I tak je rozlišení limitováno vlnovou délkou použitého světla. (b) Chybějící Fourieriovy komponenty obrazu jsou totiž ztraceny v exponenciálně ubývajících modech (tzv. evanescentní vlně), viz modrá křivka. (c) Veselagova rovinná čočka spolehlivě zobrazí všechny paprsky do ohniska. (d) Evanescentní vlna je dokonce zesílena a přispívá k výslednému obrazu. Proto nezávisí rozlišovací schopnost této čočky na vlnové délce. Zdroj: Physics Today, 2004.

Další aplikace

Metamateriály jsou materiály budoucnosti a lidé jen pootevřeli dvířka k netušeným možnostem. Veselagova čočka v oblasti radiových frekvencí stejně tak jako nové typy filtrů elektromagnetických vln jsou již skutečností. Metamateriály ale mohou mít i další významné využití. Vždyť jen to, že štěrbinový rezonátor se pod vlivem elektromagnetické vlny chová jako malý pasivní magnet může znamenat revoluci v magnetických materiálech, jejich použití a výrobě. Lze očekávat vývoj levných vysoce kvalitních magnetů, které umožní nové druhy elektrických pohonů, od elektromobilů až po nové tiché a výkonné motorky pro harddisky. Nedávno experimentálně ověřená odezva metamateriálů v terahertzové oblasti může vyřešit dosavadní neexistenci vhodných detektorů v této oblasti, zejména při letištních kontrolách nebo při zobrazovacích metodách v biomedicíně s ultravysokým rozlišením. A co teprve kdyby se v budoucnosti podařilo vytvořit metamateriály v optickém oboru? Perfektní rovinné čočky by byly revolucí nejenom v astronomii.

Klip týdne: Válcová vlna v metamateriálu

Válcová vlna v metamateriálu. V animaci vidíte počítačovou simulaci šíření válcové vlny na rozhraní dvou prostředí (rozhraní je zobrazeno bílou čarou). V levé části je prostředí s indexem lomu +1, ve kterém je generována válcová vlna. Ta se šíří přes rozhraní do druhého prostředí, které má v první části klipu index lomu +2 a dochází tedy k běžnému lomu na rozhraní. V druhé části klipu je napravo prostředí s indexem lomu −2. Válcová vlna se šíří do metamateriálu se záporným indexem lomu a přirozeným způsobem je fokusována. Toho se využívá u tzv. Veselagovy čočky. Metamateriály je zatím možné uměle připravit jen pro radiové frekvence. Zdroj: Faustus, Mefisto3D. (avi, 7 MB).

Odkazy