|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Kelvin, mol, kandela – poslední tři jednotky soustavy SI
Martin Žáček
O posledních třech jednotkách soustavy SI pojednáme najednou, neboť mají leccos společného. Tím společným jmenovatelem je skutečnost, že veličiny těmto jednotkám příslušející mají statistický charakter. U teploty a látkového množství je toto zřejmé již ze samotné povahy obou veličin. Nemají totiž smysl pro jedinou částici a jsou definovány právě na základě mnohačásticové struktury každého makroskopického objektu. U teploty jde o vztah k průměrné energii připadající na jeden stupeň volnosti částice, kde přepočítací koeficient je Boltzmannova konstantaBoltzmannova konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se k nebo kB. Řadí se mezi fundamentální fyzikální konstanty. V roce 2018 byla (s platností od 20. května 2019) Boltzmannova konstanta zafixována na hodnotě k = 1,380 649×10−23 JK−1. Tato hodnota určuje kelvin – teplotní stupeň Kelvinovy škály v soustavě jednotek SI. S molární plynovou konstantou R souvisí vztahem R = NAk, kde a NA je Avogadrova konstanta.. Látkové množství je ještě jednodušší. Z mikroskopického pohledu jde totiž jen o pouhé množství částic. Skoro nás to přivádí k otázce, proč je tedy látkové množství zavedeno jako fyzikální veličina. Vždyť se jedná o celočíselný počet částic a fyzikální veličiny jsou obvykle spojité. Jak ale naznačíme dále v souvislosti s Avogadrovou konstantouAvogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI., je (makroskopická) realizace této jednotky stejná jako u ostatních veličin, spojitých i z mikroskopického pohledu. Toto číslo se totiž nikdy přesně nedozvíme, budeme se k němu vždy jen víceméně přibližovat a také proto se místo termínu Avogadrovo číslo doporučuje používat název Avogadrova konstantaAvogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI.. Kandelu, jednotku svítivosti, jsme si nechali nakonec. Její statistický charakter je totiž nejméně zřejmý. Vždyť jde o záření, nikoliv o nějakou statistiku částic. Když si však uvědomíme, že energie světla je předávána po dále nedělitelných kvantech nazývaných fotony, můžeme se na fotometrické veličiny dívat rovněž jako na makroskopicky se projevující energie velkého množství částic světelného záření, fotonů. Do celkové svítivosti se ale nesčítá pouze energie, záleží rovněž na frekvenci záření. To zohledňuje koeficient světelné účinnosti záření, který lze vypočítat integrací přes normalizovanou citlivost oka u denního, tzv. fotopického vidění.
Uzavřeme tedy tento úvodní odstavec tvrzením, že první čtyři jednotky soustavy SI (metr, kilogram, sekunda a ampér) odpovídají fundamentálním veličinám, jimiž jsme schopni popisovat a měřit jevy jak v mikrosvětě tak v makrosvětě, dalším třem jednotkám, kelvinu, kandele a molu, odpovídají veličiny, které mají smysl jen v makrosvětě a projeví se vždy v souvislosti se statistickým průměrováním na velkém počtu molekul, atomů či kvant záření.
Definice posledních tří jednotek SI
| veličina | jednotka | značka | definice |
|---|---|---|---|
| teplota | kelvin | K |
Kelvin je 1/273,16 část termodynamické teploty trojného bodu vody. |
| látkové množství | mol | mol |
Mol je takové látkové množství, které obsahuje tolik elementárních jedinců, kolik je atomů obsažených ve 12 g uhlíku 12C. |
| svítivost | kandela | cd |
Kandela je svítivost monochromatického zdroje o frekvenci 540×1012 Hz, jehož zářivost v daném směru činí 1/683 wattů na steradián. |
Definice veličin souvisejících se zářením
| veličina | jednotka | značka | definice |
|---|---|---|---|
| zářivý tok (výkon) |
W | P |
Energie vyzářená za jednotku času. |
| spektrální zářivý tok |
W/m | Pλ |
Energie vyzářená za jednotku času na interval vlnové délky, Pλ =dP/dλ. |
| hustota zářivého toku (intenzita) |
W/m2 | He |
Energie vyzářená za jednotku času jednotkovou plochou. |
| zářivost | W/sr | Ie |
Energie vyzářená za jednotku času do jednotky prostorového úhlu. |
| světelný tok | lumen (cd·sr) |
Φ |
Zářivý tok hodnocený normálním lidským okem, Φ = ∫KλPλdλ. Koeficient K se nazývá světelná účinnost záření. |
| svítivost | cd (lm/sr) |
I |
Světelný tok vyzářený do jednotky prostorového úhlu. |
| osvětlení | lux (cd/m2) |
E |
Plocha má osvětlení 1 lx, jestliže na 1 m2 plochy dopadne rovnoměrně rozložený světelný tok 1 lm. |
| světelná účinnost záření | lm/W | K |
Koeficient úměrnosti mezi veličinami založenými na energetické bilanci vyzařování a mezi korespondujícími veličinami souvisejícími s citlivostí lidského oka. |
|
Boltzmannova konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se k nebo kB. Řadí se mezi fundamentální fyzikální konstanty. V roce 2018 byla (s platností od 20. května 2019) Boltzmannova konstanta zafixována na hodnotě k = 1,380 649×10−23 JK−1. Tato hodnota určuje kelvin – teplotní stupeň Kelvinovy škály v soustavě jednotek SI. S molární plynovou konstantou R souvisí vztahem R = NAk, kde a NA je Avogadrova konstanta. Avogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI. Molární plynová konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se R. Řadí se mezi odvozené fyzikální konstanty a lze ji vyjádřit pomocí základních fyzikálních konstant vztahem R = NAk, kde k je Boltzmannova konstanta a NA je Avogadrova konstanta. Poslední určená hodnota molární plynové konstanty je R = 8,314472 JK−1mol−1 s relativní chybou 1,7×10−7. |
Kelvin
Zatímco jako standardní používaná teploměrná stupnice pro běžné použití a pro většinu technických aplikací je Celsiova stupnice dělená ve stupních, soustava SI používá jako jednotku kelvin. Stupeň Celsia a kelvin jsou stejně velké jednotky, rozdíl je pouze ten, že teplota v kelvinech je udávána v absolutní stupnici, která má definovánu nulovou hodnotu při teplotě absolutní nuly. Je ještě řada dalších stupnic, stále používaných v různých částech světa. Historicky existovala dříve Celsiova stupnice navržena švédským astronomem Andersem Celsiem v roce 1742. Původně však měla hodnotu 0 stupňů pro bod varu vody a 100 stupňů pro bod jejího tání. William Thomson Kelvin, britský matematik a fyzik, navrhl svou absolutní teplotní stupnici, založenou na nově objevených zákonech termodynamiky, po více jak sto letech od zavedení Celsiovy stupnice, v roce 1848.

William Thompson známý jako lord Kelvin,
tvůrce absolutní teplotní stupnice.
Kelvin je nyní definován jako 1/273,16 část termodynamické teploty trojného bodu vody. Od roku 1968 byl u jednotky kelvin odstraněn symbol ° a teplota se zapisuje například jako 300 K, čte se 300 kelvinů. Do roku 1954 byla Celsiova stupnice definována pomocí teploty tání a vypařování vody, čemuž odpovídaly hodnoty 0 °C a 100 °C a absolutní stupnice měřená v kelvinech byla odvozena ze stupnice Celsiovy tak, aby měla v absolutní nule hodnotu 0 K a velikost jednotky měly obě stupnice stejnou. Po tomto roce se vzájemný vztah obou stupnic stal opačným. Absolutní stupnice měřená v kelvinech začíná nadále v bodě 0 K a má definován druhý bod, trojný bod vody, jehož hodnota je definitoricky předepsána. Tím je určena velikost jednotky, která u obou stupnic zůstává nadále stejná. U Celsiovy stupnice byla předepsána absolutní nula jako hodnota −273,15 °C, čímž je definováno vzájemné posunutí obou stupnic. Celsiova stupnice je od tohoto roku tedy naopak odvozena ze stupnice Kelvinovy.
Vztah mezi teplotou, vnímanou makroskopickými přístroji a energií přiřazenou jednotlivým atomům a molekulám udává ekvipartiční teorém, známý ze statistické fyziky jako E1 = 1/2 kT, kde E1 je průměrná energie jednoho stupně volnosti a k je Boltzmannova konstantaBoltzmannova konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se k nebo kB. Řadí se mezi fundamentální fyzikální konstanty. V roce 2018 byla (s platností od 20. května 2019) Boltzmannova konstanta zafixována na hodnotě k = 1,380 649×10−23 JK−1. Tato hodnota určuje kelvin – teplotní stupeň Kelvinovy škály v soustavě jednotek SI. S molární plynovou konstantou R souvisí vztahem R = NAk, kde a NA je Avogadrova konstanta.. Hodnotu Boltzmannovy konstantyBoltzmannova konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se k nebo kB. Řadí se mezi fundamentální fyzikální konstanty. V roce 2018 byla (s platností od 20. května 2019) Boltzmannova konstanta zafixována na hodnotě k = 1,380 649×10−23 JK−1. Tato hodnota určuje kelvin – teplotní stupeň Kelvinovy škály v soustavě jednotek SI. S molární plynovou konstantou R souvisí vztahem R = NAk, kde a NA je Avogadrova konstanta., která je zahrnuta do Planckova vyzařovacího zákona, vypočetl jako první v roce 1900 Max Planck, když ji pro formulaci zmíněného zákona potřeboval. Výpočet provedl ze slavné rovnice známé jako Boltzmannův princip, definující vztah mezi entropií jako mírou neuspořádanosti a termodynamickou pravděpodobností realizace daného makroskopického stavu soustavy.
Měření Boltzmannovy konstanty
Pro experimentální stanovení Boltzmannovy konstantyBoltzmannova konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se k nebo kB. Řadí se mezi fundamentální fyzikální konstanty. V roce 2018 byla (s platností od 20. května 2019) Boltzmannova konstanta zafixována na hodnotě k = 1,380 649×10−23 JK−1. Tato hodnota určuje kelvin – teplotní stupeň Kelvinovy škály v soustavě jednotek SI. S molární plynovou konstantou R souvisí vztahem R = NAk, kde a NA je Avogadrova konstanta. bylo vypracováno několik metod, z nichž některé jsou shodné s metodami měření Avogadrovy konstantyAvogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI.. Jsou to metody založené na Brownově pohybu, torzních kmitech zrcátka a podobně a jsou uvedeny dále, v odstavci zabývajícím se látkovým množstvím. Tyto metody jsou však málo přesné a nesplňují současné požadavky na přesnost fyzikálních konstant. Proto se nyní Boltzmannova konstantaBoltzmannova konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se k nebo kB. Řadí se mezi fundamentální fyzikální konstanty. V roce 2018 byla (s platností od 20. května 2019) Boltzmannova konstanta zafixována na hodnotě k = 1,380 649×10−23 JK−1. Tato hodnota určuje kelvin – teplotní stupeň Kelvinovy škály v soustavě jednotek SI. S molární plynovou konstantou R souvisí vztahem R = NAk, kde a NA je Avogadrova konstanta. určuje výpočtem ze vztahu R = NAk, kde R je molární plynová konstanta. Molární plynovou konstantuMolární plynová konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se R. Řadí se mezi odvozené fyzikální konstanty a lze ji vyjádřit pomocí základních fyzikálních konstant vztahem R = NAk, kde k je Boltzmannova konstanta a NA je Avogadrova konstanta. Poslední určená hodnota molární plynové konstanty je R = 8,314472 JK−1mol−1 s relativní chybou 1,7×10−7. je možné měřit zjišťováním závislosti tlaku plynu na objemu. Aby se eliminovaly odchylky plynu od ideálnosti, vypočte se extrapolace na nulový tlak, při kterém by se plyn choval v limitním případě přesně ideálně. Od roku 1972 je známa ještě přesnější metoda, neboť v tomto roce bylo publikováno použití metody přesného měření rychlosti zvuku v akustickém interferometru, při níž se využívá závislost rychlosti zvuku na tlaku a hustotě, dané Laplaceovým vzorcem. Rychlost zvuku se měří při různých tlacích a poté se podobně extrapoluje na nulový tlak. Poslední určená hodnota molární plynové konstanty je R = 8,314472 K−1mol−1 s relativní chybou 1,7×10−7. Tomu odpovídá hodnota Boltzmannovy konstantyBoltzmannova konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se k nebo kB. Řadí se mezi fundamentální fyzikální konstanty. V roce 2018 byla (s platností od 20. května 2019) Boltzmannova konstanta zafixována na hodnotě k = 1,380 649×10−23 JK−1. Tato hodnota určuje kelvin – teplotní stupeň Kelvinovy škály v soustavě jednotek SI. S molární plynovou konstantou R souvisí vztahem R = NAk, kde a NA je Avogadrova konstanta. k = 1,3806505 ×10−23 J K−1 s relativní chybou 1,8×10−6. Chyba Boltzmannovy konstanty je větší, neboť se na ní podílí jak chyba v určení molární plynové konstanty R, tak chyba určení Avogadrovy konstantyAvogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI. NA.
Mol
Mol, jednotka látkového množství, je používána v chemii a ve fyzikální chemii v podstatě tak, že jde o vhodně definované množství látky, které bude tvořit jednotku. Pro některé případy je totiž účelné vztáhnout některé veličiny nikoliv k hmotnosti (pak hovoříme o měrných podílech) ale právě k látkovému množství, jehož změna je pak spojena se změnou vnitřní energie, kde koeficient úměrnosti je tzv. chemický potenciál. Při některých chemických reakcích se totiž látkové množství může měnit i při konstantní hmotnosti a to je spojeno se změnou vnitřní energie. Množství veličiny vztažené k jednotkovému látkovému množství nazýváme molárním množstvím. Počet částic v jednotce látkového množství se nazývá Avogadrova konstantaAvogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI.. Byla zavedena na počátku 19. století, kdy Dalton, Gay-Lussac a Avogadro došli na základě výsledků svých výzkumů k závěru, že látka má svou vnitřní částicovou strukturu. Rozborem Gay-Lussacova zákona a Daltonových výsledků dospěl Avogadro k závěru, že stejné objemy různých plynů obsahují za téhož tlaku a téže teploty stejný počet molekul (Avogadrův zákon, 1811). Na této úměrnosti spočívala důležitá metoda měření atomových hmotností. Tehdy se pro množství látky používal pojem grammolekula popř. gramatom, který vyjadřoval takové množství látky v gramech, kolik činila její relativní atomová hmotnost. Později byl tento pojem nahrazen molem. Jednotka mol je definována jako množství látky, které obsahuje tolik elementárních jedinců, kolik je atomů obsažených ve 12 g uhlíku 12C. Tato definice byla přijata usnesením XIV. Generální konference pro váhy a míry v roce 1971 a v roce 1980 byla ještě zpřesněna požadavkem, že atomy uhlíku nesmí být vázané a musí být v základním stavu. 1 mol uhlíku složeného pouze z izotopu 12C má tedy podle definice hmotnost přesně 12 g, ale 1 mol přirozené směsi izotopů uhlíku bude nepatrně těžší, jeho hmotnost je přibližně 12,011 g. A tuto hodnotu atomové hmotnosti najdeme také v chemických tabulkách. Zajímavý je úhrnný náboj jednoho molu elektronů, který se v absolutní hodnotě nazývá Faradayova konstanta, vyskytující se ve vztazích v souvislosti s elektrolýzou. Její hodnota je přibližně F = 96 485 C mol−1
Měření Avogadrovy konstanty
Nejstarší metody měření Avogadrovy konstanty jsou založeny na experimentálním studiu Brownova pohybu (R. Brown, anglický botanik). Tento jev studoval intenzivně na začátku 20. století J. B. Perin, který vyvinul metodu, jak následným statistickým vyhodnocením vizuálně měřeného pohybu Brownovy částice pomocí optického mikroskopu zjistit velikosti a množství molekul v daném objemu. Na základě této nové teorie a prvních experimentů získal Perin jednu z prvních experimentálních hodnot Avogadrovy konstantyAvogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI. jako 6,0×1023 mol−1. Další zpřesnění metody je založené na torzním Brownově pohybu, při kterém se vyhodnocují nepravidelné torzní kmity rotačního systému s malým lehkým zrcátkem, zavěšeným na tenkém křemenném vlákně o průměru několik mikrometrů. Zrcátko pak má jediný stupeň volnosti a jeho střední energie je rovna podle ekvipartičního teorému 1/2 kT, kde k je Boltzmannova konstantaBoltzmannova konstanta – konstanta vyskytující se ve stavové rovnici pro ideální plyn a v mnoha dalších rovnicích termodynamiky. Značí se k nebo kB. Řadí se mezi fundamentální fyzikální konstanty. V roce 2018 byla (s platností od 20. května 2019) Boltzmannova konstanta zafixována na hodnotě k = 1,380 649×10−23 JK−1. Tato hodnota určuje kelvin – teplotní stupeň Kelvinovy škály v soustavě jednotek SI. S molární plynovou konstantou R souvisí vztahem R = NAk, kde a NA je Avogadrova konstanta.. Ta je pro malé kmity rovna střední potenciální energii, ve které se vyskytuje střední hodnota kvadrátu úhlové výchylky od rovnovážné polohy. To je veličina, kterou lze získat ze statistického zpracování časového průběhu úhlových výchylek zrcátka, což lze samozřejmě provést pomocí odraženého paprsku mnohem přesněji, než pozorováním pohybu Brownovy částice v optickém mikroskopu.
Jiného druhu je metoda založená na radioaktivním rozpadu. Metoda spočívá ve zjištění počtu atomů ve vzorku radioaktivní látky měřením počtu radioaktivních rozpadů v nějakém časovém intervalu. Pokud známe poločas rozpadu T, je pak známá i rozpadová konstanta λ a počet atomů ve vzorku N lze spočítat z rozpadové rovnice −dN = λNdt. Z různých důvodů je však přesnost metody malá, srovnatelná s metodou založenou na Brownově pohybu. Měření je zatíženo nepřesnostmi v určení odhadu účinnosti detektoru, který udává jaký podíl rozpadlých částic je detekován. Největší a prakticky neodstranitelná chyba spočívá v tom, že nikdy neměříme s preparátem, který by neobsahoval již nějaká rozpadlá jádra, jejichž počet je neznámý.
Nejpřesnější metodou pro experimentální stanovení Avogadrovy konstantyAvogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI. je metoda rentgenové difrakce. Její princip spočívá v určení mřížkové konstanty pomocí rentgenové difrakce, při které dochází k maximu v odraženém rentgenově záření při určitém, tzv. Braggově úhlu (Lawrence Bragg, 1890-1971). Tento úhel závisí na vzdálenosti krystalografických rovin od sebe a princip je stejný jako v optice při difrakci na dvou planparalelních optických rozhranních. Rozdíl je jen v tom, že k témuž jevu dochází v jiném oboru spektra elektromagnetického záření. K určení vlnové délky rentgenového záření byly postupně vyvinuty interferometry, umožňující její stanovení s chybou menší než 1 ppm. Původně byla měření prováděna na krystalech kamenné soli. Pro přesná měření se však v současné době sůl nepoužívá. Nejpřesnější hodnoty této konstanty se získávají měřením na křemíku (Si) a kalcitu (CaCO3).
Poslední, nejpřesněji stanovená hodnota Avogadrovy konstantyAvogadrova konstanta – konstanta udávající počet molekul, popřípadě jiných částic, v látkovém množství jeden mol. Značí se NA. Někdy se také nesprávně označuje jako Avogadrovo číslo. Nejpřesnější metody jejího měření byly založeny na rentgenové difrakci aplikované na vzorky monokrystalů křemíku nebo kalcitu. V roce 2018 byla (s platností od 20. května 2019) Avogadrova konstanta zafixována na hodnotě NA = 6,022 140 76×1023 mol−1. Tato hodnota určuje látkové množství jednoho molu v soustavě SI. je rovna NA = 6,0221415×1023 mol−1 s relativní chybou 1,7×10−7.
Kandela
Kandela je definována od roku 1979 jako svítivost monochromatického zdroje o frekvenci 540×1012 Hz, jehož zářivost v daném směru činí 1/683 wattů na steradián. Vztah mezi světelným tokem, jehož jednotkou je lumen, a svítivostí je takový, že bodový světelný zdroj má svítivost 1 kandela, vyzařuje-li do prostorového úhlu 1 steradián světelný tok 1 lumen. Podle definice kandely tedy světelnému toku o výkonu 1 watt monochromatického světla téže frekvence odpovídá přesně 683 lumenů. Uvedená frekvence odpovídá vlnové délce 555 nm, na níž má výše zmíněná normalizovaná křivka citlivosti oka pro fotopické vidění maximum. Předchozí definice byla založená na vyzařování světla podle Planckova zákona při teplotě tuhnoucí platiny. Byla nahrazena na XVI. Generální konferenci pro míry a váhy definicí současnou, z důvodu malé dosažitelné relativní přesnosti, asi jen 5×10−3.
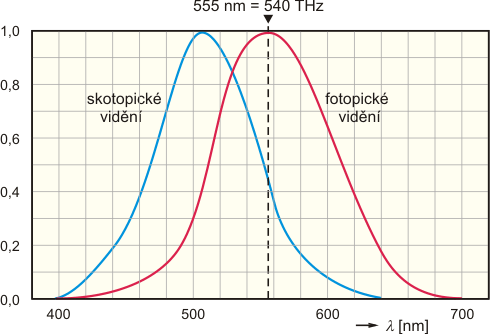
Normalizovaná křivka citlivosti lidského oka, červená křivka pro denní, tzv. fotopické vidění a modrá křivka pro noční, tzv. skotopické vidění. Křivka pro fotopické vidění má maximum na frekvenci 540 THz (vyznačeno čárkovanou přímkou), použité v současně platné definici jednotky svítivosti.
S kandelou není spojena přímo žádná základní fyzikální konstanta, pomocí které bychom přešli od makroskopické veličiny k jiným veličinám vhodným pro popis mikroskopických objektů, jako tomu bylo u předchozích dvou jednotek. Je to proto, že světelný tok závisí na citlivosti lidského oka, která je funkcí vlnové délky záření (na rozdíl od zářivého toku) přes koeficient úměrnosti nazývaný světelná účinnost záření. Jedinou výjimkou by bylo monochromatické světlo o vlnové délce 555 nm, pro které by byl koeficient světelné účinnosti roven jedné. Tím se vracíme zpět k definici, ve které je tato vlnová délka použita.
Odkazy
Mezinárodní úřad pro váhy a míry
Mezinárodní systém jednotek SI – NIST
OXFORD Reference – slovník vah, měr a jednotek
Infoplease – základní fyzikální jednotky
J. Brož, V. Roskovec: Základní fyzikální konstanty. SPN, Praha 1987
V. Kaizr: Měření rychlosti šíření světla, AB S1/2004
V. Kaizr: Měření univerzální gravitační konstanty, AB S2/2004
V. Kaizr: Měření Planckovy konstanty, AB S3/2004
P. Kulhánek: Pár otázek nad konstantami a jednotkami SI, AB S4/2004
