Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie.
Vydavatel: AGA (Aldebaran Group for Astrophysics)
Číslo 31 – vyšlo 2. srpna, ročník 2 (2004)
© Copyright Aldebaran Group for Astrophysics
Publikování nebo šíření obsahu je zakázáno.
ISSN: 1214-1674,
Email: bulletin@aldebaran.cz

Kvantová teleportace

Vojtěch Hála

Kvantová mechanika předpověděla řadu zajímavých vlastností mikrosvěta a je dnes nejlépe ověřenou fyzikální teorií všech dob. Lidé se postupně učí využívat zvláštnosti kvantových systémů v praktickém životě. Zařízení pro kvantovou kryptografii jsou již ke koupi a poskytují nepodmíněnou bezpečnost pro tajné informace. To znamená bezpečnost, která je garantována přírodními zákony a není podmíněna žádnými předpoklady na schopnosti útočníka. Další metou technologického vývoje jsou kvantové počítače a vše, co s nimi souvisí. Měly by umožnit řešení výpočetních úloh, které jsou pro klasické počítače nepřekonatelně náročné. Ale od principu k technologii je ještě dlouhá cesta. Jedním z problémů je přenos kvantových stavů mezi částmi počítače, k jehož řešení by měla pomoci teleportace. V roce 1997 vědci v Innsbrucku jako první provedli kvantovou teleportaci polarizačního stavu fotonu. Jejich pokusy byly mnohokrát úspěšně opakovány a inovovány, ale vždy šlo o fotony a protokol neumožňoval úspěšnost větší než jeden pokus ze čtyř. Teprve v červnu 2004 oznámily dva výzkumné týmy přesvědčivý úspěch s teleportací kvantového stavu hmotných částic. Laboratoř v Innsbrucku byla jedním z nich.

Kvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí navíc respektovat omezení kvantové mechaniky, které veličiny lze měřit současně. V dalším textu budeme kvantovým stavem rozumět jen jednu veličinu z tohoto souboru. Například základní energetický stav atomu značíme symbolem |S>, excitovaný stav symbolem |D>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně.

Superpozice stavů – kvantově mechanická kočka nemusí být jen živá nebo mrtvá, může být i "obojí zároveň". Takový stav značíme a|Ž>+b|M>, kde a a b jsou čísla vyjadřující váhu. Pokud na kočce v tomto superponovaném stavu provedeme měření, s pravděpodobností |a|² najdeme kočku živou a s pravděpodobností |b|² bude mrtvá.

Propletený stav (entanglement) – kvantový stav systému dvou a více částic, v němž nemá smysl mluvit o stavech jednotlivých složek. Například z propleteného stavu dvojice fotonů nelze vyjádřit stavy jednotlivých fotonů. Značíme |A₁B₂>+|X₁Y₂>, což znamená, že najdeme-li první částici ve stavu A, je druhá ve stavu B. Je-li první ve stavu X, pak druhá je ve stavu Y. Nelze ale měřit stav jedné částice aniž bychom ovlivnili druhou.

Kolaps vlnové funkce – je-li kvantový systém v superponovaném stavu, nemůžeme jeho stav přímo zjistit. Při měření v určité bázi si systém náhodně vybere některý z bázových stavů a skokem do něj přejde. Říkáme, že jeho vlnová funkce zkolabovala. Například měření na stavu |0>+|1> způsobí s 50 % pravděpodobností přechod systému do stavu |0> a se stejnou pravděpodobností do stavu |1>.

Bellovy stavy – 4 propletené stavy dvojice qubitů.

|Ψ₁> = |0₁0₂> + |1₁1₂>
|Ψ₂> = |0₁0₂> − |1₁1₂>
|Φ₁> = |0₁1₂> + |1₁0₂>
|Φ₂> = |0₁1₂> − |1₁0₂>

Bellovy stavy tvoří bázi 4-rozměrného Hilbertova prostoru.

Hilbertův prostor – úplný lineární vektorový prostor se skalárním součinem. V kvantové teorii odpovídá každý kvantový stav paprsku v Hilbertově prostoru (všem nenulovým násobkům nějakého prvku). Lineární kombinace prvků odpovídají superpozici stavů. Vlastnosti Hilbertova prostoru umožňují hovořit o změnách stavu systému v geometrických pojmech, jako jsou projekce, rotace, zrcadlení apod.

Unitární transformace – změna stavu kvantového systému, která odpovídá rotaci nebo zrcadlení v Hilbertově prostoru.

Alice a Bob – tradiční jména pro komunikující osoby užívaná v kryptografii.

Scénář teleportace

Pojem teleportace znamená, že chceme přenášet nějaký objekt nepřímo. Místo něj budeme přenášet jen informaci o něm a na straně příjemce podle ní vytvoříme objekt identický s původním. Klasická (nekvantová) teleportace předpokládá, že na vstupním objektu provedeme měření, klasickým kanálem odešleme získanou informaci a podle ní objekt rekonstruujeme. Potíž je v tom, že kvantová mechanika nedovoluje získat měřením plnou informaci o klasickém stavu objektu. Nicméně v roce 1993 odvodil Charles Bennett teleportační protokol, který umožňuje přenést kvantový stav, aniž bychom jej znali. Přenášená informace bude mít dvě části – kvantovou a klasickou. Kvantová část se "přenáší" okamžitě pomocí měření na jednom qubitu z propleteného páru stavů. Klasická informace může být předána třeba telefonem nebo jinou konvenční cestou, přičemž rychlost přenosu je shora omezena rychlostí světla.

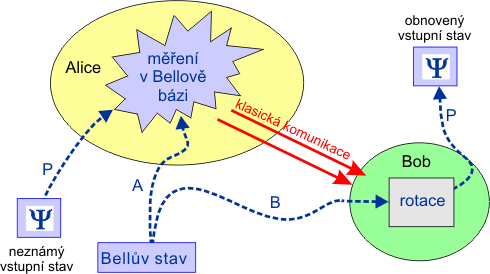
Scénář kvantové teleportace

Scénář kvantové teleportace.

Vstupem procesu je atom P v neznámém stavu |Ψ>=a|S>+b|D>, který chce Alice teleportovat Bobovi. Dále ještě před vlastní teleportací musíme připravit entanglovaný pár atomů A a B v Bellově stavu. Jednu složku páru (A) odneseme na stranu Alice, druhou složku (B) k Bobovi. Při teleportaci nejprve Alice provede s atomy A a P měření v Bellově bázi a jako výsledek měření zjistí jeden ze 4 možných Bellových stavů (|Ψ₁>, |Ψ₂>, |Φ₁> nebo |Φ₂>). Zároveň se při měření promítne stav |Ψ> do stavu atomu A. Díky kvantové propletenosti se tato změna okamžitě projeví i na atomu B, který má Bob. Ovšem aby Bob mohl rekonstruovat původní stav |Ψ>, potřebuje navíc znát výsledek měření Alice. Musí se s ní tedy domluvit nějakou klasickou cestou. Na základě této informace už může Bob na svém atomu B provést takovou unitární transformaci, která vede do stavu |Ψ>. V tu chvíli je atom B nerozlišitelný od původního P a teleportace se povedla.

Podivuhodné je, že ani klasická, ani kvantová část přenášené informace sama o sobě neříká nic o stavu |Ψ>. Když Alice provede měření, dojde okamžitě ke kolapsu propleteného páru, ale dokud se Bob nedozví výsledek měření, nemůže si toho všimnout. Bude-li Bob v tu chvíli měřit, všechny Bellovy stavy páru pro něj mají stejnou pravděpodobnost. Kolaps je sice nelokální, ale nepřenáší žádnou informaci. A výsledky měření, které Alice získala, by samy o sobě také Bobovi nebyly k ničemu, neboť pro stejný stav |Ψ> jsou pokaždé jiné.

Dále poznamenejme, že při měření v Bellově bázi na straně Alice přejde atom P ze stavu |Ψ> do jiného. Proto není možné touto cestou "klonovat" atomy – původní objekt před teleportací zanikne.

Protokol dřívějších pokusů s fotony se nezabýval analýzou Bellových stavů. Alice jen zjišťovala, zda se objeví právě ten Bellův stav, při němž Bob nemusí provádět žádné rotace pro rekonstrukci stavu |Ψ>. Ve zbylých 3 případech ze 4 byl teleportovaný stav ztracen. Letos realizované protokoly zahrnují podmíněné rotace a v ideálním případě tedy nabízí úspěšnost 100 %.

Laboratorní provedení

Skupina kvantové optiky a spektroskopie v Innsbrucku provedla teleportaci na iontech vápníku ⁴⁰Ca⁺. Tři ionty jsou drženy asi 5 μm od sebe v tzv. Paulově lineární pasti, která je kombinací statických a oscilujících elektrických polí. Qubity jsou reprezentovány superpozicí základního stavu |S> a excitovaného |D>, který má dobu života asi 1,16 sekundy. Pro manipulaci slouží přesně vyladěné a zaměřené laserové paprsky. Při měření stavu je daný atom krátce ozářen laserem a zjišťuje se jeho luminiscence.

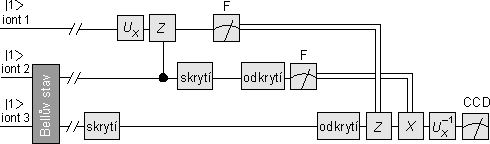
Teleportační protokol z Innsbrucku

Teleportační protokol realizovaný v Innsbrucku (F – fotonásobič)
Dvojitá čára značí přenos klasické informace.

Bellův stav dvojice iontů 2 a 3 je připraven pomocí série pulzů, která využívá propletení excitačního stavu iontů s pohybovým stavem dvojice. Poté je iont 3 speciální technikou "schován" – jeho stav je změněn tak, aby ho neovlivňovaly další pulzy. Iont 1 je připraven do zvoleného stavu |Ψ> a jeho teleportace může začít. Jako první se na iontech 1 a 2 provede operace CNOT v Bellově bázi (hradlo Z v obrázku), která jejich stavy proplete. Iont 2 je schován a na iontu 1 se změří luminiscence. Pak se odkryje a změří iont 2. Nakonec je odkryt iont 3 a podle výsledků měření na něj jsou či nejsou aplikovány rotace Z a X. Tím přejde do stavu |Ψ> a je k dispozici pro další pokusy. Životnost použitého Bellova stavu je přes 100 milisekund. Vlastní teleportace může proběhnout kdykoli v této době a trvá asi 2 ms.

Jak poznáme, že se teleportace povedla? Iont 1 byl připraven ze základního stavu do |Ψ> nějakou operací U_x. Když na cílovém iontu 3 provedeme inverzní operaci U_x⁻¹, měl by být zpět v základním stavu. Atomy v základním stavu lze detekovat pomocí luminiscence. Skupina provedla 1 200 takových experimentů a úspěšnost byla kolem 75 %. Lze ukázat, že klasická teleportace neumožňuje úspěšnost větší než 67 %, takže byla prokázána kvantová povaha procesu. Čtvrtinová chybovost je způsobena nechtěnou interakcí iontů s okolím, která je technickým problémem.

Ionty v pasti

Kvantový registr ze tří iontů v Paulově lineární pasti.
Ionty v základním stavu vykazují luminiscenci, která je vidět na CCD kameře.
Foto: Institut für Experimentalphysik, Universität Innsbruck.

Nezávisle na Innsbrucku provedli teleportační pokusy také v Národním institutu pro standardy a technologie (NIST) v USA. Použili dva základní stavy velmi jemné struktury iontů berylia ⁹Be⁺ a odlišnou techniku. Místo schovávání iontů vytvořili 8 oddělených pastí, mezi kterými jsou vybrané ionty přesouvány aplikací přesně voleného elektrického napětí. Operace v jedné pasti pak nenarušují stav iontů v sousedních pastech. Úspěšnost amerických experimentů byla také asi 75 %.

Aplikace

O využití kvantové teleportace k přemisťování makroskopicky velkých předmětů, neřku-li živých bytostí, dnes nemůže být ani řeči. Technické potíže s dokonale přesnou manipulací takovým množstvím různých částic jsou ohromné. Uvedený protokol navíc přenáší jen hodnotu jedné pozorovatelné veličiny, nikoliv kompletní kvantový stav. Na druhou stranu sny o kvantových počítačích začínají nabývat konkrétních tvarů. Výše popsané pokusy potvrzují, že ionty zachycené v lineárních pastech jsou technicky vhodnou reprezentací qubitů a kvantových registrů. Kvantová teleportace představuje řízený přenos informací mezi qubity a může být použita jako kvantové dráty pro komunikaci mezi částmi počítače libovolné velikosti.

Přístroje pro kvantovou teleportaci

Aparatura pro kvantovou teleportaci.
Foto: Institut für Experimentalphysik, Universität Innsbruck.

Detail iontové pasti

Detail iontové pasti, ve které probíhá teleportace.
Obrázek byl pořízen jedním z oken, které se používá pro optickou manipulaci s ionty.
Foto: Institut für Experimentalphysik, Universität Innsbruck.

Odkazy