Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 43 – vyšlo 27. října, ročník 1 (2003) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

43/2003

Topologie vesmíru – může být vesmír jako ementál?

Petr Kulhánek

Když Arno Penzias a Robert Wilson objevili v roce 1965 reliktní záření, netušili, jaký dopad bude jejich objev mít na budoucí fyziku. Reliktní záření je záření, které se oddělilo od látky 380 000 let po Velkém třesku a nese v sobě odkaz toho, jak vesmír vypadal v dávné minulosti. Záření má dnes již nízkou teplotu (zhruba 3 stupně nad absolutní nulou) a vlnovou délku v mikrovlnné oblasti. Záření podrobně zkoumala družice COBE (Cosmic Background Explorer) vypuštěná v roce 1989 a v posledním roce sonda WMAP (Wilkinson Microwave Anisotropy Probe) vypuštěná v roce 2001. Reliktní záření není ve všech směrech stejně teplé, v některých směrech nalezneme teplejší a v některých chladnější skvrny. Rozdíl teplot je velmi nepatrný - řádově pouhá jedna stotisícina stupně. Ale současná technika dokáže tyto skvrny (odborně fluktuace) pečlivě sledovat. Právě tyto skvrny jsou jakýmsi paleolitickým otiskem struktur raného vesmíru. Jejich průzkumem je možné určit stáří vesmíru, zastoupení různých složek a zdá se, že i celkový tvar (topologii) vesmíru. Pojďme ale začít od počátku.

Geometrie - geometrie vesmíru je lokálně určována obecnou relativitou, čas a prostor jsou zakřiveny přítomností těles a v tomto zakřiveném časoprostoru se tělesa pohybují po geodetikách. Topologie - nauka o globálních vlastnostech a struktuře množin, v našem případě o chování vesmíru jako celku. Za topologicky ekvivalentní považujeme množiny, které lze spojitě deformovat jednu na druhou. Genus topologie - číslo, které charakterizuje danou topologii z hlediska počtu "děr" nebo "držadel". Genus se určuje pomocí skupin křivek, které nelze stáhnout do bodu (jsou natažené kolem díry či držadla). Kosmická krystalografie - jde o způsob zobrazování konečné (kompaktní) topologie za pomoci vyplnění prostoru opakujícím se základním útvarem. Jde o podobný proces jako skládání krystalu z elementárních opakujících se buněk. Geodetika - nejrovnější možná dráha v zakřiveném časoprostoru. Jednoduše souvislá množina - množina, která nevypadá jako "ementál". Nemá žádné díry ani držadla, každou uzavřenou křivku lze stáhnout do bodu. Parametr Ω - podíl hustoty vesmíru ku kritické hustotě, v našem vesmíru je přibližně roven jedné, tj. vesmír je téměř plochý. Sféra posledního rozptylu - horizont, na kterém bychom pomyslně viděli oddělení záření od hmoty. Ve vzdálenějším pohledu již nevidíme reliktní záření, protože záření silně interagovalo s hmotou a neexistovalo samostatně. Reliktní záření (CMB - Cosmic Microwave Background) - záření, které se od hmoty oddělilo 380 000 let po vzniku vesmíru, dnes má teplotu 2,73 K a z jeho fluktuací usuzujeme na vlastnosti našeho vesmíru.

Geometrie vesmíru

Geometrie vesmíru je určována rozložením hmoty ve vesmíru. Hmota a energie zakřivují čas a prostor kolem sebe a v tomto pokřiveném světě se pohybují částice po nejrovnějších možných drahách - geodetikách. Míru zakřivení časoprostoru je možné určit z obecné relativity navržené A. Einsteinem v roce 1916. Z geometrického hlediska mohou nastat tři případy, které odvodil v roce 1922 ruský vědec A. Fridman a které si představujeme pomocí jednoduché dvourozměrné analogie (zakřivené plochy):

Již Fridman věděl že toto dělení nic nevypovídá o celkové topologii (globálním tvaru) našeho vesmíru. Fridman ukázal, že pokud je vesmír jednoduše souvislý (každou křivku v něm lze stáhnout do bodu, nejsou zde "díry"), potom je kladně zakřivený vesmír konečný a záporně i nulově zakřivený vesmír je nekonečný. Jednoduše souvislou množinou není třeba duše automobilu nebo ementál. Fridman věděl, že pokud by vesmír nebyl jednoduše souvislý, může být konečný i pokud má nulovou či zápornou křivost. Albert Einstein prý kdysi na Fridmanovy návrhy odvětil, že vesmír přece nemůže vypadat jako ementál a nepřipustil možnost existence jiného než jednoduše souvislého vesmíru.

Topologie vesmíru

Obecná relativita pomáhá určit lokální vlastnosti vesmíru, ale neřeší, jak vesmír vypadá jako celek. Právě vesmírná topologie je oborem, který se bouřlivě rozvíjí několik posledních let a snaží se určit celkový vzhled našeho vesmíru. Podobně jako nerosty mohou existovat v několika základních krystalografických strukturách, může mít vesmír, podle současných teorií, jen některé topologické varianty. Někdy se tyto úvahy nazývají kosmická krystalografie. Pojďme se nejprve pro jednoduchost na chvíli zabývat jen dvourozměrnou topologií obdélníku a jejím zobrazením.

Příklad – dvourozměrný vesmír z obdélníku

Představme si placaté bytosti, které žijí jen v rovině obdélníku. Znají dva směry, ale neznají třetí - výšku. Z obdélníku můžeme vytvořit pomocí ztotožňování jeho protilehlých hran čtyři topologické útvary:

Jak si tyto obdélníkové 2D vesmíry představit? Existují celkem tři způsoby. První jsme právě použili. Ztotožňování předem stanovených hran. Druhou možností je využít našich třírozměrných zkušeností a začít lepit z obdélníku kosmické origami. Obdélník ale musí být z nějaké tvarovatelné hmoty, takové, aby šel deformovat. První vesmír povede po stočení papíru a slepení hran na válcovou plochu, druhý na Möbiův pásek. U třetího musíme ve válci ještě slepit horní a dolní hranu, dostaneme útvar podobný pneumatice nazývaný v topologii toroid. Není jednoduše souvislý, existují křivky, které nelze stáhnout do bodu, genus prostoru je roven jedné. A čtvrtý? Tady budeme mít s lepením problémy i v třírozměrném světě, jde o útvar nazývaný Kleinova láhev. Kosmické origami je pro nás snadno představitelné, ale pouze v dvourozměrném světě. V třírozměrném vesmíru již nic takového provést nemůžeme, nemůžeme se odstěhovat mimo vesmír do nějaké čtvrté dimenze a začít lepit skládanku.

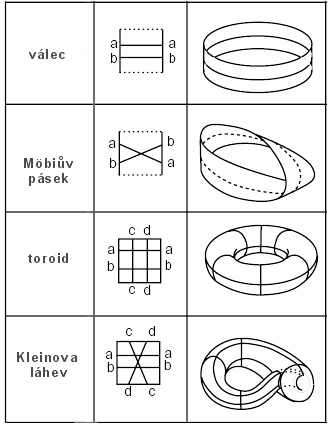
Ztotožňování hran ve 2D topologii a nadhled na útvar ve 3D.

Další způsob představy konečného vesmíru je nejelegantnější a vychází z toho, co takový pozorovatel v konečném vesmíru uvidí. Uvidí totiž mnohonásobné obrazy své i svého okolí, jakoby v zrcadlové síni. I kdyby byl v celém vesmíru sám, uvidí mnoho postav. Pohne-li se, pohnou se postupně všechny postavy, počká-li dostatečně dlouho. Když bude chytrý, zjistí, že jeho vesmír je konečný a vidí stále svůj obraz v různých fázích vývoje. Této představě můžeme říkat dláždění, chceme-li. Vesmír jsme vydláždili z opakujících se obdélníků, můžeme to provést například i z opakujících se šestiúhelníků. Jde to ale i z osmiúhelníků, nemůžeme s nimi sice vydláždit rovinu, ale konstantně záporně zakřivený prostor, ve kterém jsou vrcholové úhly menší než v rovině, ano! Vznikne známý topologický útvar, který je podobný dvoutoroidu (jsou v něm dvě díry, kolem kterých nestáhneme křivku do bodu), genus útvaru je roven dvěma.

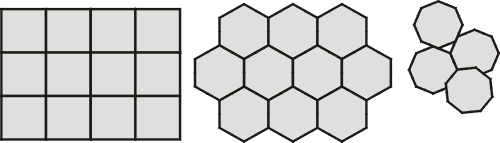
Znázornění uzavřeného vesmíru s nulovou křivostí pomocí dláždění čtverci a šestiúhelníky. Prostor s nulovou křivostí osmiúhelníky nelze vydláždit.

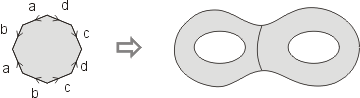
Dláždění osmiúhelníky v prostoru s konstantní zápornou křivostí

Třírozměrná topologie

Zobrazit třírozměrný zakřivený svět, navíc ještě jako celek, tj. jeho topologii, je velmi nesnadný oříšek. Snad nejjednodušší metodou pro konečné uzavřené vesmíry je použít dláždění, skládat vesmír z mnohostěnů, pravidelně se opakujících (jejich některé stěny jsou ztotožněny). Tento postup vede na nekonečné množství možností. Uvážíme-li ale vesmíry s nejmenším objemem a vyhovující obecné relativitě, počet možností výrazně klesá. První pokus o klasifikaci těch nejjednodušších případů provedl W. P. Thurston pro hyperbolické geometrie (zápornou křivost) a existuje kompletní klasifikace pro sférické geometrie (kladnou křivost). Konečných vesmírů, které by mohly přicházet v úvahu a jsou z hlediska kosmologie zajímavé, je méně než 20. Nejčastěji se zkoumá následujících pět:

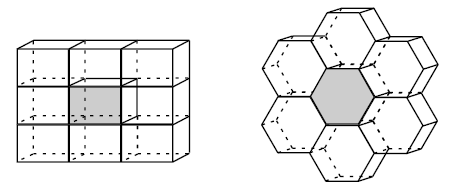
Konečné vesmíry s nulovou křivostí vydlážděné z kvádrů a šestibokých hranolů.

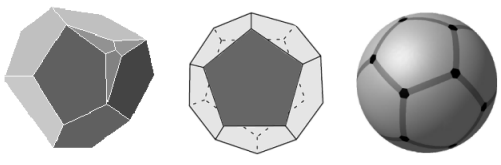
Základní mnohostěny Weeksova prostoru, Poincarého prostoru (dvanáctistěn), napravo je sférický dvanáctistěn.

V třírozměrných konečných vesmírech vidíme stále se opakující obraz v různých fázích vývoje. Kdo ví, zda některá ze vzdálených galaxií, které pozorujeme, není naše vlastní před dávnými časy.

Fluktuace reliktního záření

Vraťme se nyní k fluktuacím reliktního záření, které byly popsány v úvodu. Díky kvantovým procesům je raný vesmír neklidný a jeví zárodky budoucích struktur. V době oddělení záření od hmoty se prvopočáteční fluktuace chovají jako zvukové vlny v zárodečné látce, vesmír jako by celý zvučel podivnými zvukovými vlnami. Průchod světla těmito vlnami znamená procházení fotonů různým gravitačním potenciálem a jejich nepatrný ohřev či ochlazení. Tyto teplejší a chladnější skvrny právě pozorujeme v reliktním záření jako otisk dávných časů. Podobně jako zvuk u hudebního nástroje můžeme rozložit na základní harmonické frekvence, můžeme i fluktuace reliktního záření rozložit do takzvaných sférických harmonických. To si lze představit jako statistické sledování procentuálního zastoupení skvrn určité úhlové velikosti. Výsledkem je křivka zvaná výkonové spektrum (viz Milan Červenka: Zvuk raného vesmíru). Právě charakter fluktuací bude silně záviset na topologii vesmíru, pokud je vesmír malý a konečný. Proto se pečlivě zkoumají fluktuace reliktního záření naměřené sondou WMAP a v těchto dnech probíhají intenzivní pokusy určit topologii našeho vesmíru.

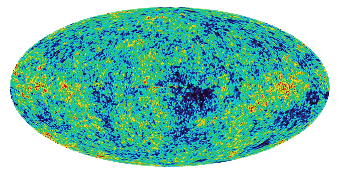
Mapa teplotních fluktuací reliktního záření pořízená sondou WMAP.

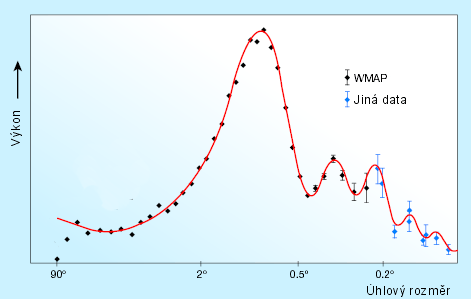
Výkonostní spektrum fluktuací (WMAP). Nejčastější
fluktuace mají úhlový rozměr 1°.

Současný stav

Zjištěné fluktuace v reliktním záření odpovídají velmi dobře modelu plochého nekonečného vesmíru až do fluktuací o velikosti zhruba 60°. Jakékoli teplotní korelace však mizí na větších škálách. Co to znamená? Žádná zvuková vlna nemůže mít nikdy vlnovou délku větší než je prostor, ve kterém se rozvinula. Jen v nekonečném vesmíru by se mohly vyskytovat i velmi nízké frekvence. Absence nízkofrekvenčních vln (korelací fluktuací s velkými úhlovými rozměry) by tak měla znamenat konečnost našeho vesmíru!

9. října 2003 pětice vědců z Francie a USA (Jean-Pierre Luminet, Jeffrey R. Weeks, Alain Riazuelo, Roland Lehoucq, Jean-Phillippe Uzan) publikovala v dopisech časopisu Nature sdělení, že fluktuacím reliktního záření měřeného sondou WMAP odpovídá ze všech navrhovaných topologií nejblíže konečný vesmír s velmi malou kladnou křivostí, Ω = (1,012÷1,014),  s topologickou strukturou založenou na Poincarého sférických dvanáctistěnech. Podle tohoto modelu by měl být vesmír pospojován tak, že protilehlé stěny dvanáctistěnu jsou totožné. Nikdy v takovém světě nenarazíme na žádnou hranici, i když je ve skutečnosti konečný. Rozměry vesmíru by měly být zhruba 70 miliard světelných let, stáří 13,7 miliard let.

Mnohonásobný obraz ve vesmíru
pospojovaném z mnohostěnů.

Je třeba si uvědomit, že jde o jeden z mnoha navržených modelů, který v tuto chvíli nejlépe odpovídá měřeným datům. K jeho potvrzení či vyvrácení bude ale třeba ještě několika týdnů až měsíců tvrdé práce vědců. Jsou navrženy další testy modelu, například vyhledávání kružnic podobných fluktuací, které by se měly vyskytovat na průsečíku sfér posledního rozptylu s protilehlými stěnami elementárního mnohostěnu Zdá se, že data z WMAP budou dostatečně podrobná. Kdyby se ukázalo, že nikoli, budeme muset vyčkat až na měření z ještě přesnější sondy Planck, jejíž start je plánován na rok 2007. Pokud by se uvedená topologie vesmíru potvrdila, šlo by bezesporu o jeden z nejvýznamnějších okamžiků moderní kosmologie a pravděpodobně fyziky vůbec.

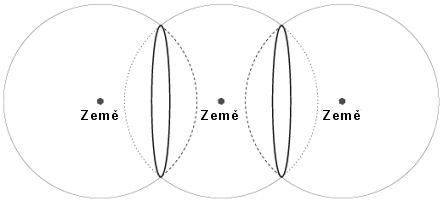
Test vyhledáváním kružnic podobných fluktuací na průsečících
sfér posledního rozptylu v mnohonásobném obrazu vesmíru.

A bonus na závěr: pokud jste hraví a chcete si vyzkoušet chování extravagantních topologií formou hry, stáhněte si určitě program SnapPea, jehož původním autorem je Jefferson Weeks, jeden z předních současných kosmologů. Další autoři program přepracovali pro nejrůznější počítačové platformy, takže si může pohrát opravdu každý.

Odkazy