Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 21 – vyšlo 26. května, ročník 1 (2003) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

21/2003

Kvantové počítače

Petr Kulhánek

Od zkonstruování prvního počítače uplynulo již více jak 60 let. V roce 1941 sestrojil německý inženýr Konrad Zuse prapředka dnešních počítačů. Zažili jsme bouřlivý rozvoj výpočetní techniky. Měnila se forma zápisu dat od děrných pásek a děrných štítků přes magnetická média a kompaktní disky. Měnila se i velikost počítačů od obřích sálových monster po dnešní malé a výkonné počítače.

Právě miniaturizace elektroniky nabírá obrovského tempa a zdá se, že ji nic nezastaví. Zdání ale klame. Svět malých rozměrů má své zákony odlišné od světa, na který jsme si zvykli my lidé. Jde o nekomutující kvantový svět, ve kterém AB není BA, ve kterém samo měření ovlivňuje stav systému, a ve kterém neplatí booleovská logika.

Svět počítačů, ve kterém je zápis založen na posloupnosti nul a jedniček, nelze miniaturizovat donekonečna. Již brzy narazíme na principiální bariéru a při další miniaturizaci přestanou platit zákony, na jejichž principu fungují dnešní počítače. Je to konec? Finální stanice, za kterou již není možné jít? Ne, je to teprve začátek! Začátek počítačů nové generace založených na kvantových principech, kdy přirozená paralelizace algoritmů je vlastností hardwaru samotného. Pojďme nyní nahlédnout pod pokličku kuchyně budoucích počítačů.

Faktorizace - rozklad čísla na součin prvočísel. Interference - skládání vln z několika zdrojů. V daném místě se sčítají amplitudy vln. Jsou-li v protifázi, může dojít k vyrušení výsledné vlny. V detekčním přístroji se detekuje intezita vlny, která je kvadrátem amplitudy. Jaderná magnetická rezonance - spiny atomových jader mohou konat precesní pohyb kolem silokřivek silného magnetického pole. Tento pohyb může být vyvolán rezonančním průchodem elektromagnetické vlny vhodné frekvence. Kvantová interference - skládání amplitud pravděpodobnosti několika možností. Amplitudy se mohou vyrušit, potom hovoříme o destruktivní interferenci. Pravděpodobnosti dějů jsou kvadrátem amplitud pravděpodobností. Kvantový počítač - Počítač využívající „hardwarově“ kvantově mechanické vlastnosti částic, například elektronů nebo atomových jader. Kvantový počítač provádí operace s qubity, tedy s více stavy současně. Tím je výpočet mnohonásobně efektivnější než u klasického počítače. Qubit (kvantový bit) - základní jednotka informace podléhající kvantové logice.  Základní informace 0 nebo 1 je nesena částicí v obou stavech až do provedení měření.

Kvantová interference

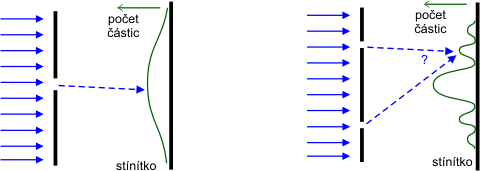
Začněme velmi jednoduchým experimentem popsaným v každé učebnici kvantové mechaniky. Představme si částice dopadající na otvor v desce (štěrbinu). Za štěrbinou je stínítko, na kterém budeme registrovat dopadající částice. Může jít například o fotony a fotografickou desku. Počet dopadlých částic bude mít maximum proti štěrbině a bude zhruba sledovat křivku na obrázku vlevo. Co když budou štěrbiny dvě? Obraz se výrazně změní. Na stínítku budou místa, na které nedopadne žádná částice. Proč? Matematické vysvětlení je snadné. Sčítají se totiž amplitudy pravděpodobností a tím dojde ke kvantové interferenci. Zkrátka podobně jako u vln se některé možnosti vyruší. Je to pro nás nezvyklé, ale takový mikrosvět je. Když zakryjeme jednu ze dvou štěrbin, dojde k paradoxnímu jevu. Nedochází k destruktivní interferenci a do místa, kam nedopadaly žádné částice nyní některé dopadnou. Méně je více! Do místa, kam při dvou otevřených štěrbinách nedopadla žádná částice, při jedné otevřené štěrbině částice dopadnou.

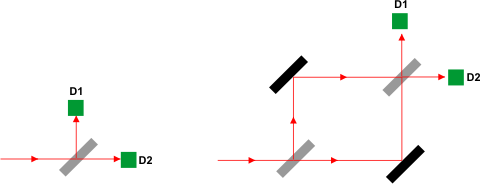
Popišme si ještě jeden obdobný experiment. Světlo se šíří přes polopropustné zrcadlo podle obrázku nalevo. Do detektorů D1 a D2 bude dopadat stejné množství fotonů. Nyní přidejme další zrcadla podle obrázku napravo. Fotony již mají dvě možné cesty, jak se dostat do každého z detektorů (stejně jako u dvouštěrbinového experimentu). Zdálo by se, že do obou detektorů by mělo dopadat stejné množství fotonů. Nikoli. Postavíme-li detektory do správného místa, nedopadne do detektoru D2 žádný foton. Důvod je stejný: destruktivní interference amplitud pravděpodobnosti obou drah. Podobně jako u dvouštěrbinového experimentu: jednu cestu stačí znemožnit (odebereme zrcadlo, do dráhy dáme překážku) a do detektoru D2 začnou dopadat fotony.

Superpozice stavů a kvantový výpočet

V kvantové teorii se u dvouštěrbinového experimentu mohla částice na stínítko dostat libovolnou z obou štěrbin. Vzhledem ke kvantové interferenci amplitud pravděpodobnosti si můžeme představit, že procházela oběma štěrbinami současně. Skutečný stav částice je směsicí obou možných stavů. Který z nich má částice, zjistíme až pomocí registračního přístroje. Tím ale narušíme interferenční obrazec. Zakryjeme-li například jednu štěrbinu, dozvíme se sice, kterým otvorem částice prolétla, ale nebudeme již pozorovat interferenční obrazec, zásadně ovlivníme měřením samotný systém. Na stejném principu je založeno kvantové počítání. Představme si systém, který se může vyskytovat ve dvou různých stavech (označme je například 0 a 1 podle analogie s klasickým zápisem informace). U makroskopických zapisovacích médií lze rozlišit od sebe zápisy nul a jedniček. Kdybychom to nedokázali, nebudeme umět zápis přečíst. Postupnou miniaturizací ale dojdeme jednou do situace, kdy začnou dominovat kvantové vlastnosti. Systém bude v superpozici obou stavů (0 i 1) a teprve akt měření rozhodne, zda jde o stav 0 či o stav 1. Systém tak nese paralelně informace o obou stavech. Výsledkem aktu měření bude hodnota 0 nebo 1, ale tuto hodnotu poznáme až měřením, které zcela naruší daný stav systému. Takovýto dvoustavový kvantový systém je základní jednotkou informace kvantového počítání, která se nazývá kvantový bit neboli qubit. Nepodléhá Booleově logice, ale elementárním zákonům kvantové teorie, tzv.kvantové logice.

Poznámka pro čtenáře ovládající Diracovu symboliku. U dvouštěrbinového experimentu je amplituda pravděpodobnosti přechodu z počátečního stavu | p > do koncového stavu | k > rovna skalárnímu součinu

< k | p >  =  < k | 1 >< 1 | p >  +  < k | 2 >< 2 | p >  =  A₁ + A₂

Jak vidíme, lze ji napsat jako součet amplitudy průchodu první a druhou štěrbinou. Sčítají se amplitudy pravděpodobnosti. Operátor | 1 >< 1 | a opeátor | 2 >< 2 | představují projekční operátory průchodu první a druhou štěrbinou, jejich součet dá jednotkový operátor. Celková pravděpodobnost je kvadrátem amplitudy a bude se skládat ze součtu pravděpodobností průchodu první a druhou štěrbinou a interferenčního členu:

P = |A₁ + A₂|²  =  |A₁|² + |A₂|² + A₁^*A₂ + A₁A₂^*  = P₁ + P₂ + P_int

Path Integrals – integrály po drahách

V polovině minulého století přišel Richard Feynman se zajímavou myšlenkou. Pokud se částice může mezi dvěma místy šířit po několika možných drahách, šíří se současně po každé z nich. Každé možné trajektorii můžeme přiřadit kvantovou amplitudu pravděpodobnosti. Skutečná pravděpodobnost je potom kvadrátem součtu amplitud pravděpodobností všech trajektorií. Feynman dokonce vyvinul k sečtení amplitud všech trajektorií speciální matematický nástroj – spojitě nekonečně rozměrné integrály, tzv. integrály po drahách. Kvantová částice se jakoby paralelně šíří po všech možných dráhách. Pravděpodobnost většiny z nich se destruktivní interferencí vyruší. Zůstanou jen některé trajektorie, které jsou možné i v klasické mechanice. Kvantovým systémům je proto vlastní vnitřně zabudovaný paralelismus. Logika postavená na zákonech kvantové teorie je přirozenou cestou paralelní.

Shorův algoritmus

Za jednu z nejobtížnějších úloh ve výpočetní technice je považováno nalezení účinného algoritmu pro faktorizaci velkých čísel. Například číslo 1 295 952 můžeme napsat jako součin prvočísel 2³×3×7²×19×29.

Jestliže ve dvojkové soustavě číslo zapíšeme pomocí posloupnosti n jedniček a nul, má nejlepší dosud nalezený algoritmus exponenciální obtížnost (rozumějte závislost potřebného výpočetního času na n).

V roce 1994 bylo pomocí tohoto algoritmu faktorizováno číslo zapsané z posloupnosti 129 nul a jedniček. Výpočet provádělo paralelně 1600 pracovních stanic po dobu osmi měsíců. Se stejnou výpočetní technikou by faktorizace čísla složeného z tisíce nul a jedniček trvala 10²⁵ let. Je zřejmé, že tato úloha není stávající technikou řešitelná a právě toho využívají kódovací systémy bank a vojenských organizací.

Právě ve stejném roce, v roce 1994, navrhl P. W. Shor algoritmus faktorizace postavený na kvantové logice. Jeho obtížnost je zhruba kvadratická!!! To je dáno právě přirozeným paralelizmem v kvantové logice. Pokud bychom sestrojili počítač postavený na kvantové logice, bylo by dešifrování tajných zpráv a stávajících bankovních kódů jednoduchou záležitostí.

Simulace kvantových počítačů na stávajícím hardware

Kvantovou logiku můžeme samozřejmě simulovat i na obyčejném PC. Simulace je jen poněkud nevýhodná a mimořádně obtížná, protože vzájemná korelace mezi kvantovými bity (qubity) a klasickými bity je zcela odlišná. Veškeré paralelní procesy probíhající naráz při kvantovém výpočtu musíme řešit v Booleově logice separátně. Výsledek je tak velmi žalostný. Mimořádně pomalý kód. Nicméně už dnes si můžeme hrát s kvantovou logikou a zkoušet si její vlastnosti na běžných počítačích. Dokonce byl vyvinut speciální programovací jazyk QCL (Quantum Computing Language). Poslední stabilní verze je 0.4.3 a poslední dostupná beta verze 0.5.0. Syntaxe jazyka je podobná jazyku C.

Skutečný kvantový počítač

Skutečný kvantový počítač musí být samozřejmě realizován na skutečném kvantovém systému. Od roku 1999 probíhají intenzívní pokusy na mnoha předních vědeckých pracovištích. Především jde o QUIC (Quantum Information Center) bohatě podporovaný armádní organizací DARPA, dále LANL (Los Alamos National Laboratory), MIT (Massachussettss Institute of Techology) a CALTECH (California Technology). Jaké jsou publikované výsledky? Velice nadějné. Podařilo se uskutečnit přenosy qubitů pomocí chladných iontů zlata zachycených v lineární iontové pasti, kterou se šíří vibrace v podobě fononů indukovaných soustavou laserů. Jiný systém je založen i na zcela odlišném principu, ve kterém se qubity pohybují v jaderných spinech kapalného roztoku alaninu nebo trichlóretylénu. Roztok je vnořen do silného magnetického pole. Procházející elektromagnetická vlna potom budí precesní pohyb spinů známý jako jaderná magnetická rezonance. Objevují se i další systémy.

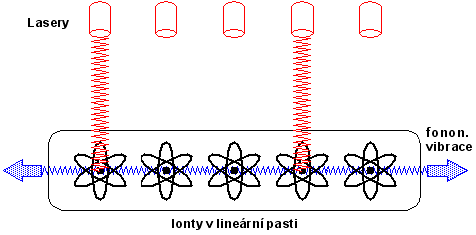
Lidstvo bude určitě muset překonat počáteční problémy s hardwarovou architekturou kvantového počítače, s interakcí qubitů s okolím, která vede k dekoherenci a vzniku chyb, i se spoustou dalších potíží, které při konstrukci kvantového počítače vyvstanou. V současnosti jsme svědky zrodu kvantového hardwaru. Zatím velice primitivního, ale přece jen je jasné, že zrod použitelných kvantových počítačů je otázkou velmi krátkého času.

Odkazy